The Kitchin Research Group

The van der Waal equation of state is:

\(P = \frac{R T}{V - b} - \frac{a}{V^2}\).

We define the reduced pressure as \(P_r = P / P_c\), and the reduced temperature as \(T_r = T / T_c\).

So, we simply solve for V at a given \(P_r\), and then compute \(Z\). There is a subtle trick needed to make this easy to solve, and that is to multiply each side of the equation by \((V - b)\) to avoid a singularity when \(V = b\), which happens in this case near \(P_r \approx 7.5\).

from scipy.optimize import fsolve
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt

R = 0.08206
Pc = 72.9
Tc = 304.2

a = 27 * R**2 * Tc**2 / (Pc * 64)
b = R * Tc / (8 * Pc)

Tr = 1.1

def objective(V, Pr):
    P = Pr * Pc
    T = Tr * Tc
    return P * (V - b) - (R * T)  +  a / V**2 * (V - b)


Pr_range = np.linspace(0.1, 10)
V = [fsolve(objective, 3, args=(Pr,))[0] for Pr in Pr_range]

T = Tr * Tc
P_range = Pr_range * Pc
Z = P_range * V / (R * T)

plt.plot(Pr_range, Z)
plt.xlabel('$P_r$')
plt.ylabel('Z')
plt.xlim([0, 10])
plt.ylim([0, 2])

(0, 2)

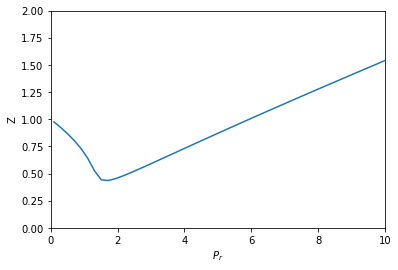
That looks like Figure 7-1 in the book. This approach is fine, but the equation did require a little algebraic finesse to solve, and you have to use some iteration to get the solution.

In this method, you have to derive an expression for \(\frac{dV}{dP_r}\). That derivation goes like this:

\(\frac{dV}{dP_r} = \frac{dV}{dP} \frac{dP}{dP_r}\)

The first term \(\frac{dV}{dP}\) is \((\frac{dP}{dV})^{-1}\), which we can derive directly from the van der Waal equation, and the second term is just a constant: \(P_c\) from the definition of \(P_r\).

They derived:

\(\frac{dP}{dV} = -\frac{R T}{(V - b)^2} + \frac{2 a}{V^3}\)

We need to solve for one V, at the beginning of the range of \(P_r\) we are interested in.

V0, = fsolve(objective, 3, args=(0.1,))
V0

3.6764763125625461

Now, we can define the functions, and integrate them to get the same solution. I defined these pretty verbosely, just for readability.

from scipy.integrate import solve_ivp

def dPdV(V):
    return -R * T / (V - b)**2 + 2 * a / V**3

def dVdP(V):
    return 1 / dPdV(V)

dPdPr = Pc

def dVdPr(Pr, V):
    return dVdP(V) * dPdPr

Pr_span = (0.1, 10)
Pr_eval, h = np.linspace(*Pr_span, retstep=True)

sol = solve_ivp(dVdPr, Pr_span, (V0,), dense_output=True, max_step=h)

V = sol.y[0]
P = sol.t * Pc
Z = P * V / (R * T)
plt.plot(sol.t, Z)
plt.xlabel('$P_r$')
plt.ylabel('Z')
plt.xlim([0, 10])
plt.ylim([0, 2])

(0, 2)

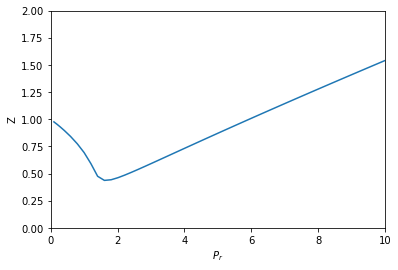
This also looks like Figure 7-1. It is arguably a better approach since we only need an initial condition, and after that have a reliable integration (rather than many iterative solutions from an initial guess of the solution in fsolve).

The only downside to this approach (in my opinion) is the need to derive and implement derivatives. As equations of state get more complex, this gets more tedious and complicated.

The whole point of automatic differentiation is to get derivatives of functions that are written as programs. We explore here the possibility of using this to solve this problem. The idea is to use autograd to define the derivative \(dP/dV\), and then solve the ODE like we did before.

from autograd import grad

def P(V):
    return R * T / (V - b) - a / V**2

# autograd.grad returns a callable that acts like a function
dPdV = grad(P, 0)

def dVdPr(Pr, V):
    return 1 / dPdV(V) * Pc

sol = solve_ivp(dVdPr,  Pr_span, (V0,), dense_output=True, max_step=h)

V, = sol.y
P = sol.t * Pc
Z = P * V / (R * T)
plt.plot(sol.t, Z)
plt.xlabel('$P_r$')
plt.ylabel('Z')
plt.xlim([0, 10])
plt.ylim([0, 2])

(0, 2)

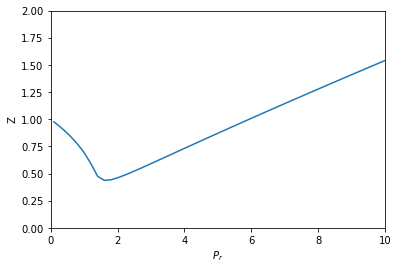
Not surprisingly, this answer looks the same as the previous ones. I think this solution is pretty awesome. We only had to implement the van der Waal equation, and then let autograd do its job to get the relevant derivative. We don't get a free pass on calculus here; we still have to know which derivatives are important. We also need some knowledge about how to use autograd, but with that, this problem becomes pretty easy to solve.

There are two small chunks of repeated code in the example above. One way to minimize the amount of repeated code is to pull these out into reusable functions. Here, we do that, and only have to repeat one function call at the end to get the system composition out.

import numpy as np
from scipy.optimize import fsolve

acetone = (14.5463, 2940.46, 237.22)
acetonitrile = (14.2724, 2945.47,224)
nitromethane = (14.2043, 2972.64, 209)

def antoine(T, A, B, C):
    T = float(T) # there is some subtle issue that comes up when T is an array,
                 # as passed in from fsolve. It needs to be a float, or you get
                 # the wrong answer.
    return np.exp(A - B / (T + C))

x = np.array([0.3, 0.45, 0.25])
P = 80

def Pvap(T):
    return np.array([antoine(T, *pars) for pars in [acetone, acetonitrile, nitromethane]])

def y(T):
    return x * Pvap(T) / P

def objective(T):
    return 1 - y(T).sum()

Tans, = fsolve(objective, 70)

yans = y(Tans) # minimal repetition of a calculation to get the composition state.

print(f'The bubble point temperature is {Tans:1.2f} degC, and the gas phase compositions are {np.round(yans, 4)}.')

The bubble point temperature is 68.60 degC, and the gas phase compositions are [ 0.5196  0.3773  0.1031].

That is a small improvement. The code is not much shorter, just reorganized for easier reuse. It would be easy in this case to also get the vapor pressures of each species at this temperature, just by calling the Pvap function. Still, it feels annoying we have to recalculate the answer to something you know must have already been known when the objective function was evaluated.

In this approach, we will use a dictionary to store the state of the objective function. The dictionary will be in the global namespace, and we will just update it each time the objective function is called.

import numpy as np
from scipy.optimize import fsolve

acetone = (14.5463, 2940.46, 237.22)
acetonitrile = (14.2724, 2945.47,224)
nitromethane = (14.2043, 2972.64, 209)

def antoine(T, A, B, C):
    return np.exp(A - B / (T + C))

x = np.array([0.3, 0.45, 0.25])

state = {}

P = 80


def objective(T, state):
    T = float(T)
    Pvap = np.array([antoine(T, *pars) for pars in [acetone, acetonitrile, nitromethane]])
    y = x * Pvap / P
    state.update({'y': y,
                  'T':  T,
                  'Pvap': Pvap,
                  'z': 1 - y.sum()})
    return state['z']

Tans, = fsolve(objective, 70, args=(state,))

print(f'The bubble point temperature is {Tans:1.2f} degC, and the gas phase compositions are {np.round(state["y"], 4)}.')
print(Tans- state['T']) # check to make sure last value from objective is the same as the solution
state

The bubble point temperature is 68.60 degC, and the gas phase compositions are [ 0.5196  0.3773  0.1031].
0.0

{'Pvap': array([ 138.5620209 ,   67.07966082,   32.98218545]),
 'T': 68.60064626680659,
 'y': array([ 0.51960758,  0.37732309,  0.10306933]),
 'z': -3.4194869158454821e-14}

What we see in the state dictionary is the result from the last time that the objective function was called. It appears that the list time it was called is also where the solution comes from, so the other variables stored here should be consistent. Now you can see we have access to both the Pvap and y composition data from the solution without needing any further computations. This approach could be easily extended to store any derived quantities that represent internal states you want. We don't store any history in this, but you could by appending to lists in the dictionary.

One feature of this is the state dictionary is updated by side effect, and you have to use the state dictionary as an argument parameter to the function.

A standard approach to tracking state data is to encapsulate it in a class. fsolve requires a callable function that returns zero at the solution. It is possible to make an object act like a callable function if we define a __call__ method on it. Then, in this method, we can set attributes on the object to keep track of the state, similar to what we did with the dictionary. Since we have a class, we can define some other special dunder methods, e.g. to print the solution. Here is one implementation.

import numpy as np
from scipy.optimize import fsolve

class Objective(object):
    acetone = (14.5463, 2940.46, 237.22)
    acetonitrile = (14.2724, 2945.47,224)
    nitromethane = (14.2043, 2972.64, 209)

    def __init__(self, x, P):
        self.x = np.array(x)
        self.P = P

    def antoine(self, T, A, B, C):
        return np.exp(A - B / (T + C))

    def __str__(self):
        s = f'The bubble point temperature is {self.T:1.2f} degC, and the gas phase compositions are {np.round(self.y, 4)}.'
        return s

    def __call__(self, T):
        T = float(T)
        self.T = T
        self.Pvap = np.array([self.antoine(T, *pars) for pars in [self.acetone, self.acetonitrile, self.nitromethane]])
        self.y = self.x * self.Pvap / self.P
        return 1 - self.y.sum()

obj = Objective(x=np.array([0.3, 0.45, 0.25]), P=80)
ans, = fsolve(obj, 60)

print(obj)

The bubble point temperature is 68.60 degC, and the gas phase compositions are [ 0.5196  0.3773  0.1031].

Similar to the state dictionary approach, there is no repeated code here, and no repeated evaluations to get to the state after the solution. This is a bit more advanced Python than the state dictionary. Note, this implementation doesn't have any checking in it, so if you try to print the object before calling fsolve, you will get an error because the attributes don't exist until after the object has been called. That is also an issue with the state dictionary above.

There are many choices you could make in constructing this example. Maybe this one has gone too far in encapsulating the antoine function as a method. That limits its reusability for another problem. On the other hand, you can reuse it for any other pressure or liquid composition of acetone, acetonitrile and nitromethane very readily.

We looked at three ways to reduce having redundant code in the solution to problems involving nonlinear algebra. The first approach is conceptually simple; you break out as much as you can into reusable functions, and then at most have repeated function calls. These computations are usually not expensive, so repeating them is mostly tedious and provides opportunities for mistakes. This is probably what I will stick to for teaching students that are just seeing this for the first time.

The second approach used a dictionary (other data structures could work too) as an argument to the objective function, and internal states were kept in the dictionary so that after the problem was solved, you have immediate access to them. This is more advanced than the first approach because it requires understanding that the dictionary is modified as a side effect of solving the problem.

Finally, we considered an object-oriented class encapsulation of the information we wanted. I consider this the most advanced Python solution, since it requires some understanding of classes, dunder methods and attributes, and how to make an instance of a class.

The last two methods seem like candidates for an advanced class in problem solving. Thoughts?

This is a common idiom to enable easy running of the doctests. This will get tangled out to the file.

if __name__ == "__main__":
    import doctest
    doctest.testmod()

So far, the Python code we have written only exists in the org-file, and in memory. Tangling is the extraction of the code into a code file.

We run this command, which extracts the code blocks marked for tangling, and expands the noweb references in them.

(org-babel-tangle)

Here is what we get:

def func(a):
    """A function to divide one by a.

    >>> func(5) == 0.2
    True

    >>> func(0)
    Traceback (most recent call last):
    ZeroDivisionError: division by zero

    >>> for i in range(1, 4):
    ...     print(func(i))
    1.0
    0.5
    0.3333333333333333


    Returns: 1 / a.
    """
    return 1 / a

if __name__ == "__main__":
    import doctest
    doctest.testmod()

That looks like a reasonable python file. You can see the doctest blocks have been inserted into the docstring, as desired. The proof of course is that we can run these doctests, and use the python module. We show that next.

Now, we can check if the tests pass in a fresh run (i.e. not using the version stored in the jupyter kernel.) The standard way to run the doctests is like this:

python test.py -v

Well, that's it! It worked fine. Now we have a python file we can import and reuse, with some doctests that show how it works. For example, here it is in a small Python script.

from test import func
print(func(3))

0.3333333333333333

There are surely some caveats to keep in mind here. This was just a simple proof of concept idea that isn't tested beyond this example. I don't know how many complexities would arise from more complex doctests. But, it seems like a good idea to continue pursuing if you like using doctests, and like using org-mode and interactive/literate programming techniques.

It is definitely an interesting way to use noweb to build up better code files in my opinion.

These blocks are used in the noweb expansions. Each block takes a variable which is the name of a block. This block grabs the body of the named src block and formats it as if it was in a REPL.

We also grab the results of the named block and format it for the doctest. We use a heuristic to detect Tracebacks and modify the output to be consistent with it. In that case we assume the relevant Traceback is on the last line.

Admittedly, this does some fragile feeling things, like trimming whitespace here and there to remove blank lines, and quoting quotes (which was not actually used in this example), and removing the ": " pieces of ob-ipython results. Probably other ways of running the src-blocks would not be that suitable for this.

(org-babel-goto-named-src-block name)
(let* ((src (s-trim-right (org-element-property :value (org-element-context))))
       (src-lines (split-string src "\n"))
       body result)
  (setq body
        (s-trim-right
         (s-concat ">>> " (car src-lines) "\n"
                   (s-join "\n" (mapcar (lambda (s)
                                          (concat "... " s))
                                        (cdr src-lines))))))
  ;; now the results
  (org-babel-goto-named-result name)
  (let ((result (org-element-context)))
    (setq result
          (thread-last
              (buffer-substring (org-element-property :contents-begin result)
                                (org-element-property :contents-end result))
            (s-trim)
            ;; remove ": " from beginning of lines
            (replace-regexp-in-string "^: *" "")
            ;; quote quotes
            (replace-regexp-in-string "\\\"" "\\\\\"")))
    (when (string-match "Traceback" result)
      (setq result (format
                    "Traceback (most recent call last):\n%s"
                    (car (last (split-string result "\n"))))))
    (concat body "\n" result)))

In calculus, we know that if we have a well-behaved function \(f(x, y)\), then it should be true that \(\frac{\partial^2f}{\partial x \partial y} = \frac{\partial^2f}{\partial y \partial y}\).

Here we use autograd to compute the mixed partial derivatives and show for 10 random points that this statement is true. This doesnt' prove it for all points, of course, but it is easy to prove for any point of interest.

def f(x, y):
    return x * y**2

dfdx = grad(f)
d2fdxdy = grad(dfdx, 1)

dfdy = grad(f, 1)
d2fdydx = grad(dfdy)

x = np.random.rand(10)
y = np.random.rand(10)

T = [d2fdxdy(x1, y1) == d2fdydx(x1, y1) for x1, y1 in zip(x, y)]

print(np.all(T))

True

fsolve often works fine without access to derivatives. In this example from here, we solve a set of equations with two variables, and it takes 21 iterations to reach the solution.

from scipy.optimize import fsolve

def f(x):
    return np.array([x[1] - 3*x[0]*(x[0]+1)*(x[0]-1),
                     .25*x[0]**2 + x[1]**2 - 1])


ans, info, flag, msg = fsolve(f, (0.5, 0.5), full_output=1)
print(ans)
print(info['nfev'])

[ 1.117 0.83 ] 21

If we add the jacobian, we get the same result with only 15 iterations, about 1/3 fewer iterations. If the iterations are expensive, this might save a lot of time.

df = jacobian(f)
x0 = np.array([0.5, 0.5])

ans, info, flag, msg  = fsolve(f, x0, fprime=df, full_output=1)
print(ans)
print(info['nfev'])

[ 1.117 0.83 ] 15

There is a similar example provided by autograd.

In this post we described how to fit a solid equation of state to describe the energy of a solid under isotropic strain. Now, we can readily compute the pressure at a particular volume from the equation:

\(P = -\frac{dE}{dV}\)

We just need the derivative of this equation:

\(E = E_0+\frac{B_0 V}{B'_0}\left[\frac{(V_0/V)^{B'_0}}{B'_0-1}+1\right]-\frac{V_0 B_0}{B'_0-1}\)

or we use autograd to get it for us.

E0, B0, BP, V0 = -56.466,   0.49,    4.753,  16.573

def Murnaghan(vol):
    E = E0 + B0 * vol / BP * (((V0 / vol)**BP) / (BP - 1.0) + 1.0) - V0 * B0 / (BP - 1.)
    return E

def P(vol):
    dEdV = grad(Murnaghan)
    return -dEdV(vol) * 160.21773  # in Gpa

print(P(V0)) # Pressure at the minimum
print(P(0.99 * V0))  # Compressed

4.44693531998e-15
0.808167684691

So it takes positive pressure to compress the system, as expected, and at the minimum the pressure is equal to zero. Seems pretty clear autograd is better than deriving the required pressure derivative.

Thermodynamics tells us that in a binary mixture the following is true:

\(0 = x_1 \frac{d \ln \gamma_1}{dx_1} + (1 - x_1) \frac{d \ln \gamma_2}{dx_1}\)

In other words, the activity coefficients of the two species can't be independent.

Suppose we have the Margules model for the excess free energy:

\(G^{ex}/RT = n x_1 (1 - x_1) (A_{21} x_1 + A_{12} (1 - x_1))\)

where \(n = n_1 + n_2\), and \(x_1 = n1 / n\), and \(x_2 = n_2 / n\).

From this expression, we know:

\(\ln \gamma_1 = \frac{\partial G_{ex}/RT}{\partial n_1}\)

and

\(\ln \gamma_2 = \frac{\partial G_{ex}/RT}{\partial n_2}\)

It is also true that (the Gibbs-Duhem equation):

\(0 = x_1 \frac{d \ln \gamma_1}{d n_1} + x_2 \frac{d \ln \gamma_2}{d n_1}\)

Here we will use autograd to get these derivatives, and demonstrate the Gibbs-Duhem eqn holds for this excess Gibbs energy model.

A12, A21 = 2.04, 1.5461  # Acetone/water https://en.wikipedia.org/wiki/Margules_activity_model

def GexRT(n1, n2):
    n = n1 + n2
    x1 = n1 / n
    x2 = n2 / n
    return n * x1 * x2 * (A21 * x1 + A12 * x2)

lngamma1 = grad(GexRT)     # dGex/dn1
lngamma2 = grad(GexRT, 1)  # dGex/dn2

n1, n2 = 1.0, 2.0
n = n1 + n2
x1 = n1 / n
x2 = n2 / n

# Evaluate the activity coefficients
print('AD:         ',lngamma1(n1, n2), lngamma2(n1, n2))

# Compare that to these analytically derived activity coefficients
print('Analytical: ', (A12 + 2 * (A21 - A12) * x1) * x2**2, (A21 + 2 * (A12 - A21) * x2) * x1**2)

# Demonstration of the Gibbs-Duhem rule
dg1 = grad(lngamma1)
dg2 = grad(lngamma2)

n = 1.0 # Choose a basis number of moles
x1 = np.linspace(0, 1)
x2 = 1 - x1
n1 = n * x1
n2 = n - n1

GD = [_x1 * dg1(_n1, _n2) + _x2 * dg2(_n1, _n2)
      for _x1, _x2, _n1, _n2 in zip(x1, x2, n1, n2)]

print(np.allclose(GD, np.zeros(len(GD))))

('AD:         ', 0.76032592592592585, 0.24495925925925932)
('Analytical: ', 0.760325925925926, 0.24495925925925924)
True

That is pretty compelling. The autograd derivatives are much easier to code than the analytical solutions (which also had to be derived). You can also see that the Gibbs-Duhem equation is satisfied for this model, at least with a reasonable tolerance for the points we evaluated it at.

Today we examined four ways to use autograd in scientific or mathematical programs to replace the need to derive derivatives by hand. The main requirements for this to work are that you use the autograd.numpy module, and only the functions in it that are supported. It is possible to add your own functions (described in the tutorial) if needed. It seems like there are a lot of opportunities for scientific programming for autograd.

The forces are where derivatives are important, and it is a reasonable question of whether hand-coded derivatives are faster or slower than autograd derivatives. We first look at the forces from ASE. The analytical forces take about the same time as the energy, which is not surprising. The same work is done for both of them.

np.set_printoptions(precision=3, suppress=True)
print(atoms.get_forces())

[[-0.    -0.    -0.   ]
 [-0.296 -0.     0.183]
 [-0.296 -0.    -0.183]
 [ 0.296 -0.     0.183]
 [ 0.296 -0.    -0.183]
 [ 0.183 -0.296 -0.   ]
 [-0.183 -0.296  0.   ]
 [ 0.183  0.296 -0.   ]
 [-0.183  0.296  0.   ]
 [-0.     0.183 -0.296]
 [ 0.    -0.183 -0.296]
 [-0.     0.183  0.296]
 [ 0.    -0.183  0.296]]

%%timeit
atoms.get_forces()
atoms.calc.results = {}

1.22 ms ± 38.7 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

Here is our auto-differentiated force function.

from autograd import elementwise_grad

def forces(pos):
    dEdR = elementwise_grad(energy)
    return -dEdR(pos)

Let's just check the forces for consistency.

print(forces(atoms.positions))

print(np.allclose(forces(atoms.positions), atoms.get_forces()))

[[-0.    -0.    -0.   ]
 [-0.296 -0.     0.183]
 [-0.296 -0.    -0.183]
 [ 0.296 -0.     0.183]
 [ 0.296 -0.    -0.183]
 [ 0.183 -0.296 -0.   ]
 [-0.183 -0.296  0.   ]
 [ 0.183  0.296 -0.   ]
 [-0.183  0.296  0.   ]
 [-0.     0.183 -0.296]
 [ 0.    -0.183 -0.296]
 [-0.     0.183  0.296]
 [ 0.    -0.183  0.296]]
True

Those all look the same, so now performance for that:

%%timeit 

forces(pos)

727 µs ± 47.1 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

This is faster than the ASE version. I suspect that it is largely because of the faster, vectorized algorithm overall.

print('autograd is {0:1.1f} times faster than ASE on forces.'.format(1.22e-3 / 727e-6))

autograd is 1.7 times faster than ASE on forces.

autograd forces are consistently 2-6 times faster than the ASE implementation. It could be possible to hand-code a faster function for the forces, if it was fully vectorized. I spent a while seeing what would be required for that, and it is not obvious how to do that. Any solution that uses loops will be slower I think.

This doesn't directly answer the question of whether this can work in production. Everything is still written in Python here, which might limit the size and length of calculations you can practically do. With the right implementation though, it looks promising.