Solving differential algebraic equations with help from autograd
Posted September 22, 2019 at 12:59 PM | categories: ode, autograd, dae | tags:
This problem is adapted from one in "Problem Solving in Chemical Engineering with Numerical Methods, Michael B. Cutlip, Mordechai Shacham".
In the binary, batch distillation of benzene (1) and toluene (2), the moles of liquid \(L\) remaining as a function of the mole fraction of toluene (\(x_2\)) is expressed by:
\(\frac{dL}{dx_2} = \frac{L}{x_2 (k_2 - 1)}\)
where \(k_2\) is the vapor liquid equilibrium ratio for toluene. This can be computed as:
\(k_i = P_i / P\) where \(P_i = 10^{A_i + \frac{B_i}{T +C_i}}\) and that pressure is in mmHg, and the temperature is in degrees Celsius.
One difficulty in solving this problem is that the temperature is not constant; it changes with the composition. We know that the temperature changes to satisfy this constraint \(k_1(T) x_1 + k_2(T) x_2 = 1\).
Sometimes, one can solve for T directly, and substitute it into the first ODE, but this is not a possibility here. One way you might solve this is to use the constraint to find \(T\) inside an ODE function, but that is tricky; nonlinear algebra solvers need a guess and don't always converge, or may converge to non-physical solutions. They also require iterative solutions, so they will be slower than an approach where we just have to integrate the solution. A better way is to derive a second ODE \(dT/dx_2\) from the constraint. The constraint is implicit in \(T\), so We compute it as \(dT/dx_2 = -df/dx_2 / df/dT\) where \(f(x_2, T) = k_1(T) x_1 + k_2(T) x_2 - 1 = 0\). This equation is used to compute the bubble point temperature. Note, it is possible to derive these analytically, but who wants to? We can use autograd to get those derivatives for us instead.
The following information is given:
The total pressure is fixed at 1.2 atm, and the distillation starts at \(x_2=0.4\). There are initially 100 moles in the distillation.
| species | A | B | C |
|---|---|---|---|
| benzene | 6.90565 | -1211.033 | 220.79 |
| toluene | 6.95464 | -1344.8 | 219.482 |
We have to start by finding the initial temperature from the constraint.
import autograd.numpy as np from autograd import grad from scipy.integrate import solve_ivp from scipy.optimize import fsolve %matplotlib inline import matplotlib.pyplot as plt P = 760 * 1.2 # mmHg A1, B1, C1 = 6.90565, -1211.033, 220.79 A2, B2, C2 = 6.95464, -1344.8, 219.482 def k1(T): return 10**(A1 + B1 / (C1 + T)) / P def k2(T): return 10**(A2 + B2 / (C2 + T)) / P def f(x2, T): x1 = 1 - x2 return k1(T) * x1 + k2(T) * x2 - 1 T0, = fsolve(lambda T: f(0.4, T), 96) print(f'The initial temperature is {T0:1.2f} degC.')
The initial temperature is 95.59 degC.
Next, we compute the derivative we need. This derivative is derived from the constraint, which should ensure that the temperature changes as required to maintain the constraint.
dfdx2 = grad(f, 0) dfdT = grad(f, 1) def dTdx2(x2, T): return -dfdx2(x2, T) / dfdT(x2, T) def ode(x2, X): L, T = X dLdx2 = L / (x2 * (k2(T) - 1)) return [dLdx2, dTdx2(x2, T)]
Next we solve and plot the ODE.
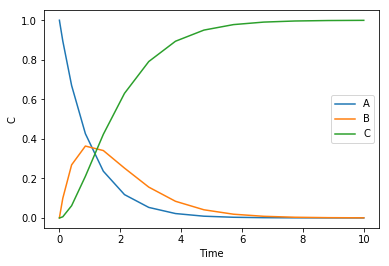
x2span = (0.4, 0.8) X0 = (100, T0) sol = solve_ivp(ode, x2span, X0, max_step=0.01) plt.plot(sol.t, sol.y.T) plt.legend(['L', 'T']); plt.xlabel('$x_2$') plt.ylabel('L, T') x2 = sol.t L, T = sol.y print(f'At x2={x2[-1]:1.2f} there are {L[-1]:1.2f} moles of liquid left at {T[-1]:1.2f} degC')
At x2=0.80 there are 14.04 moles of liquid left at 108.57 degC
<Figure size 432x288 with 1 Axes>
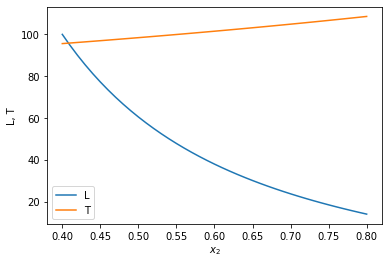
You can see that the liquid level drops, and the temperature rises.
Let's double check that the constraint is actually met. We do that qualitatively here by plotting it, and quantitatively by showing all values are close to 0.
constraint = k1(T) * (1 - x2) + k2(T) * x2 - 1 plt.plot(x2, constraint) plt.ylim([-1, 1]) plt.xlabel('$x_2$') plt.ylabel('constraint value') print(np.allclose(constraint, np.zeros_like(constraint))) constraint
True
array([ 2.22044605e-16, 4.44089210e-16, 2.22044605e-16, 0.00000000e+00,
1.11022302e-15, 0.00000000e+00, 6.66133815e-16, 0.00000000e+00,
-2.22044605e-16, 1.33226763e-15, 8.88178420e-16, -4.44089210e-16,
4.44089210e-16, 1.11022302e-15, -2.22044605e-16, 0.00000000e+00,
-2.22044605e-16, -1.11022302e-15, 4.44089210e-16, 0.00000000e+00,
-4.44089210e-16, 4.44089210e-16, -6.66133815e-16, -4.44089210e-16,
4.44089210e-16, -1.11022302e-16, -8.88178420e-16, -8.88178420e-16,
-9.99200722e-16, -3.33066907e-16, -7.77156117e-16, -2.22044605e-16,
-9.99200722e-16, -1.11022302e-15, -3.33066907e-16, -1.99840144e-15,
-1.33226763e-15, -2.44249065e-15, -1.55431223e-15, -6.66133815e-16,
-2.22044605e-16])
<Figure size 432x288 with 1 Axes>

So indeed, the constraint is met! Once again, autograd comes to the rescue in making a computable derivative from an algebraic constraint so that we can solve a DAE as a set of ODEs using our regular machinery. Nice work autograd!
Copyright (C) 2019 by John Kitchin. See the License for information about copying.
Org-mode version = 9.2.3