The Gibbs free energy of a reacting mixture and the equilibrium composition
Posted February 18, 2013 at 09:00 AM | categories: optimization | tags: thermodynamics, reaction engineering
Updated September 10, 2014 at 12:21 PM
Table of Contents
In this post we derive the equations needed to find the equilibrium composition of a reacting mixture. We use the method of direct minimization of the Gibbs free energy of the reacting mixture.
The Gibbs free energy of a mixture is defined as \(G = \sum\limits_j \mu_j n_j\) where \(\mu_j\) is the chemical potential of species \(j\), and it is temperature and pressure dependent, and \(n_j\) is the number of moles of species \(j\).
We define the chemical potential as \(\mu_j = G_j^\circ + RT\ln a_j\), where \(G_j^\circ\) is the Gibbs energy in a standard state, and \(a_j\) is the activity of species \(j\) if the pressure and temperature are not at standard state conditions.
If a reaction is occurring, then the number of moles of each species are related to each other through the reaction extent \(\epsilon\) and stoichiometric coefficients: \(n_j = n_{j0} + \nu_j \epsilon\). Note that the reaction extent has units of moles.
Combining these three equations and expanding the terms leads to:
$$G = \sum\limits_j n_{j0}G_j^\circ +\sum\limits_j \nu_j G_j^\circ \epsilon +RT\sum\limits_j(n_{j0} + \nu_j\epsilon)\ln a_j $$
The first term is simply the initial Gibbs free energy that is present before any reaction begins, and it is a constant. It is difficult to evaluate, so we will move it to the left side of the equation in the next step, because it does not matter what its value is since it is a constant. The second term is related to the Gibbs free energy of reaction: \(\Delta_rG = \sum\limits_j \nu_j G_j^\circ\). With these observations we rewrite the equation as:
$$G - \sum\limits_j n_{j0}G_j^\circ = \Delta_rG \epsilon +RT\sum\limits_j(n_{j0} + \nu_j\epsilon)\ln a_j $$
Now, we have an equation that allows us to compute the change in Gibbs free energy as a function of the reaction extent, initial number of moles of each species, and the activities of each species. This difference in Gibbs free energy has no natural scale, and depends on the size of the system, i.e. on \(n_{j0}\). It is desirable to avoid this, so we now rescale the equation by the total initial moles present, \(n_{T0}\) and define a new variable \(\epsilon' = \epsilon/n_{T0}\), which is dimensionless. This leads to:
$$ \frac{G - \sum\limits_j n_{j0}G_j^\circ}{n_{T0}} = \Delta_rG \epsilon' + RT \sum\limits_j(y_{j0} + \nu_j\epsilon')\ln a_j $$
where \(y_{j0}\) is the initial mole fraction of species \(j\) present. The mole fractions are intensive properties that do not depend on the system size. Finally, we need to address \(a_j\). For an ideal gas, we know that \(A_j = \frac{y_j P}{P^\circ}\), where the numerator is the partial pressure of species \(j\) computed from the mole fraction of species \(j\) times the total pressure. To get the mole fraction we note:
$$y_j = \frac{n_j}{n_T} = \frac{n_{j0} + \nu_j \epsilon}{n_{T0} + \epsilon \sum\limits_j \nu_j} = \frac{y_{j0} + \nu_j \epsilon'}{1 + \epsilon'\sum\limits_j \nu_j} $$
This finally leads us to an equation that we can evaluate as a function of reaction extent:
$$ \frac{G - \sum\limits_j n_{j0}G_j^\circ}{n_{T0}} = \widetilde{\widetilde{G}} = \Delta_rG \epsilon' + RT\sum\limits_j(y_{j0} + \nu_j\epsilon') \ln\left(\frac{y_{j0}+\nu_j\epsilon'}{1+\epsilon'\sum\limits_j\nu_j} \frac{P}{P^\circ}\right) $$
we use a double tilde notation to distinguish this quantity from the quantity derived by Rawlings and Ekerdt which is further normalized by a factor of \(RT\). This additional scaling makes the quantities dimensionless, and makes the quantity have a magnitude of order unity, but otherwise has no effect on the shape of the graph.
Finally, if we know the initial mole fractions, the initial total pressure, the Gibbs energy of reaction, and the stoichiometric coefficients, we can plot the scaled reacting mixture energy as a function of reaction extent. At equilibrium, this energy will be a minimum. We consider the example in Rawlings and Ekerdt where isobutane (I) reacts with 1-butene (B) to form 2,2,3-trimethylpentane (P). The reaction occurs at a total pressure of 2.5 atm at 400K, with equal molar amounts of I and B. The standard Gibbs free energy of reaction at 400K is -3.72 kcal/mol. Compute the equilibrium composition.
import numpy as np R = 8.314 P = 250000 # Pa P0 = 100000 # Pa, approximately 1 atm T = 400 # K Grxn = -15564.0 #J/mol yi0 = 0.5; yb0 = 0.5; yp0 = 0.0; # initial mole fractions yj0 = np.array([yi0, yb0, yp0]) nu_j = np.array([-1.0, -1.0, 1.0]) # stoichiometric coefficients def Gwigglewiggle(extentp): diffg = Grxn * extentp sum_nu_j = np.sum(nu_j) for i,y in enumerate(yj0): x1 = yj0[i] + nu_j[i] * extentp x2 = x1 / (1.0 + extentp*sum_nu_j) diffg += R * T * x1 * np.log(x2 * P / P0) return diffg
There are bounds on how large \(\epsilon'\) can be. Recall that \(n_j = n_{j0} + \nu_j \epsilon\), and that \(n_j \ge 0\). Thus, \(\epsilon_{max} = -n_{j0}/\nu_j\), and the maximum value that \(\epsilon'\) can have is therefore \(-y_{j0}/\nu_j\) where \(y_{j0}>0\). When there are multiple species, you need the smallest \(epsilon'_{max}\) to avoid getting negative mole numbers.
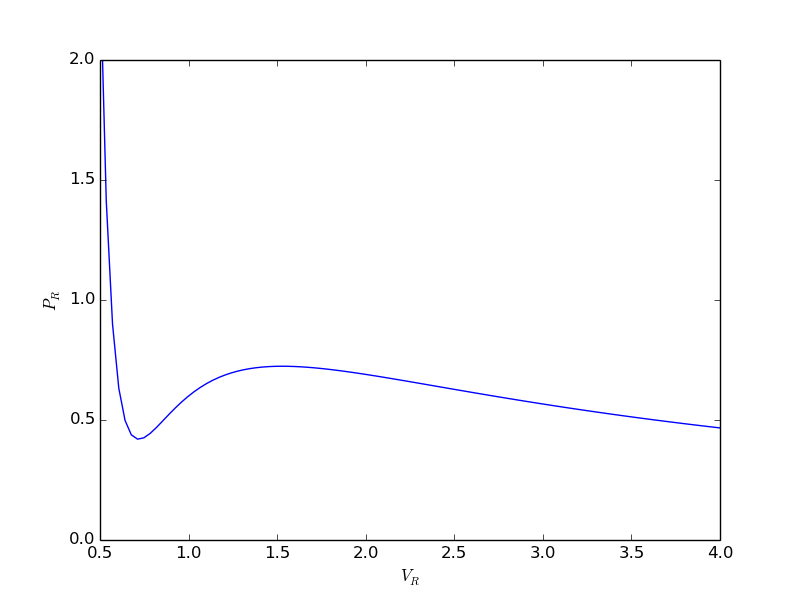
epsilonp_max = min(-yj0[yj0 > 0] / nu_j[yj0 > 0]) epsilonp = np.linspace(1e-6, epsilonp_max, 1000); import matplotlib.pyplot as plt plt.plot(epsilonp,Gwigglewiggle(epsilonp)) plt.xlabel('$\epsilon$') plt.ylabel('Gwigglewiggle') plt.savefig('images/gibbs-minim-1.png')
>>> >>> >>> __main__:7: RuntimeWarning: divide by zero encountered in log __main__:7: RuntimeWarning: invalid value encountered in multiply [<matplotlib.lines.Line2D object at 0x10b1c7710>] <matplotlib.text.Text object at 0x10b1c3d10> <matplotlib.text.Text object at 0x10b1c9b90>
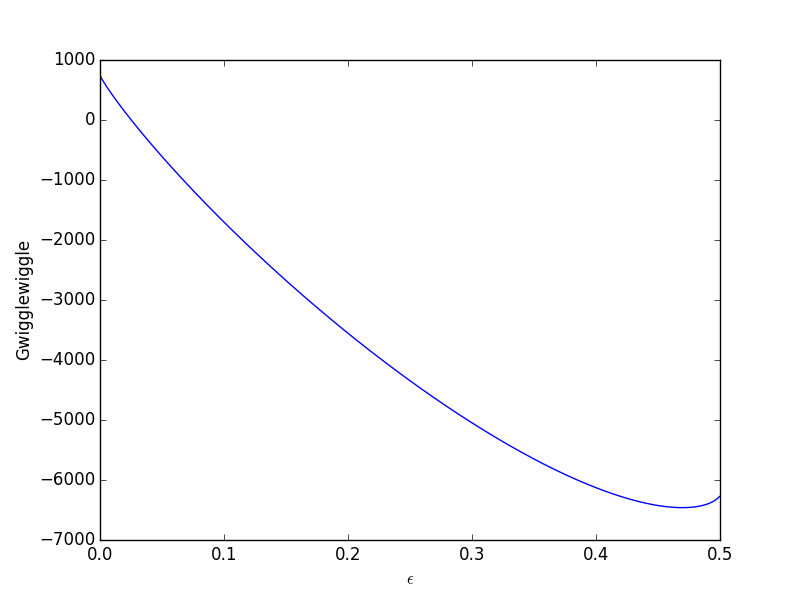
Now we simply minimize our Gwigglewiggle function. Based on the figure above, the miminum is near 0.45.
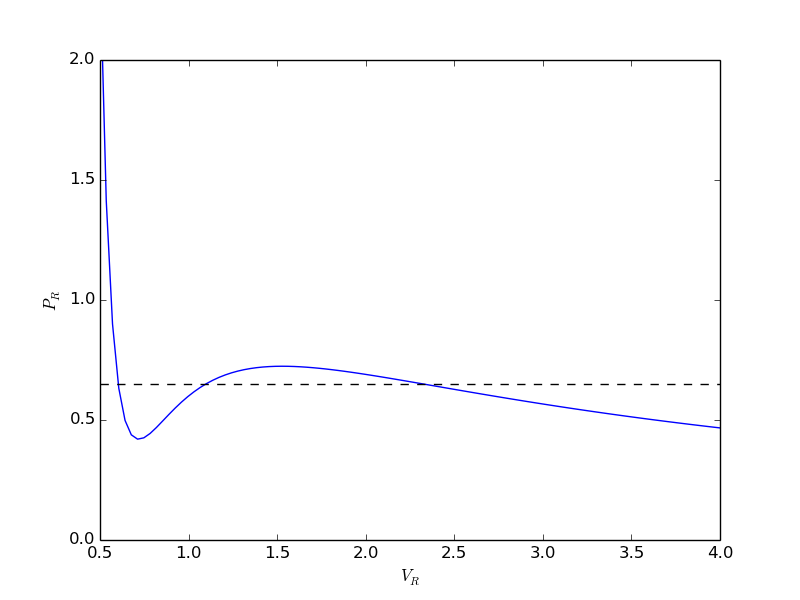
from scipy.optimize import fminbound epsilonp_eq = fminbound(Gwigglewiggle, 0.4, 0.5) print epsilonp_eq plt.plot([epsilonp_eq], [Gwigglewiggle(epsilonp_eq)], 'ro') plt.savefig('images/gibbs-minim-2.png')
>>> >>> 0.46959618249 >>> [<matplotlib.lines.Line2D object at 0x10d4d3e50>]
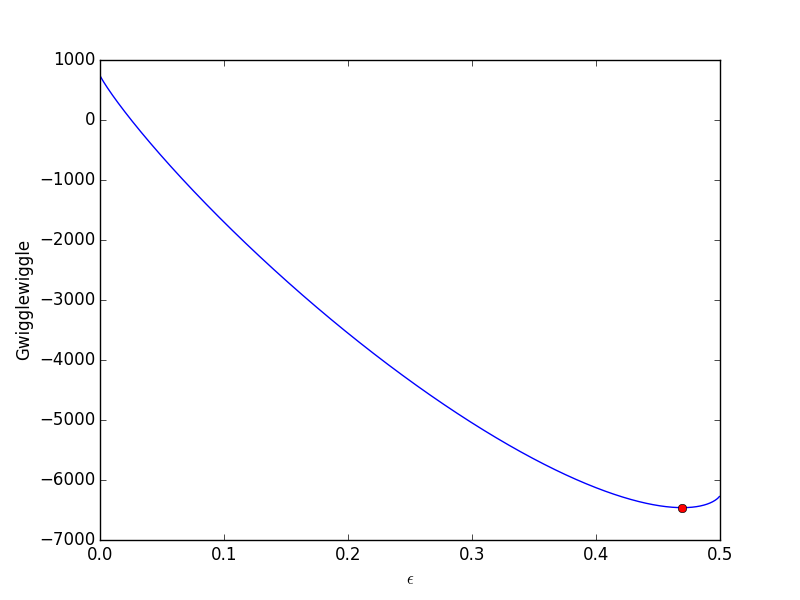
To compute equilibrium mole fractions we do this:
yi = (yi0 + nu_j[0]*epsilonp_eq) / (1.0 + epsilonp_eq*np.sum(nu_j)) yb = (yb0 + nu_j[1]*epsilonp_eq) / (1.0 + epsilonp_eq*np.sum(nu_j)) yp = (yp0 + nu_j[2]*epsilonp_eq) / (1.0 + epsilonp_eq*np.sum(nu_j)) print yi, yb, yp # or this y_j = (yj0 + np.dot(nu_j, epsilonp_eq)) / (1.0 + epsilonp_eq*np.sum(nu_j)) print y_j
>>> >>> >>> 0.0573220186324 0.0573220186324 0.885355962735 >>> ... >>> [ 0.05732202 0.05732202 0.88535596]
\(K = \frac{a_P}{a_I a_B} = \frac{y_p P/P^\circ}{y_i P/P^\circ y_b P/P^\circ} = \frac{y_P}{y_i y_b}\frac{P^\circ}{P}\).
We can express the equilibrium constant like this :\(K = \prod\limits_j a_j^{\nu_j}\), and compute it with a single line of code.
K = np.exp(-Grxn/R/T) print 'K from delta G ',K print 'K as ratio of mole fractions ',yp / (yi * yb) * P0 / P print 'compact notation: ',np.prod((y_j * P / P0)**nu_j)
K from delta G 107.776294742 K as ratio of mole fractions 107.779200065 compact notation: 107.779200065
These results are very close, and only disagree because of the default tolerance used in identifying the minimum of our function. You could tighten the tolerances by setting options to the fminbnd function.
1 Summary
In this post we derived an equation for the Gibbs free energy of a reacting mixture and used it to find the equilibrium composition. In future posts we will examine some alternate forms of the equations that may be more useful in some circumstances.
Copyright (C) 2014 by John Kitchin. See the License for information about copying.
Org-mode version = 8.2.7c