The Kitchin Research Group

Matlab post adapated from http://msemac.redwoods.edu/~darnold/math55/DEproj/sp02/AbeRichards/slideshowdefinal.pdf

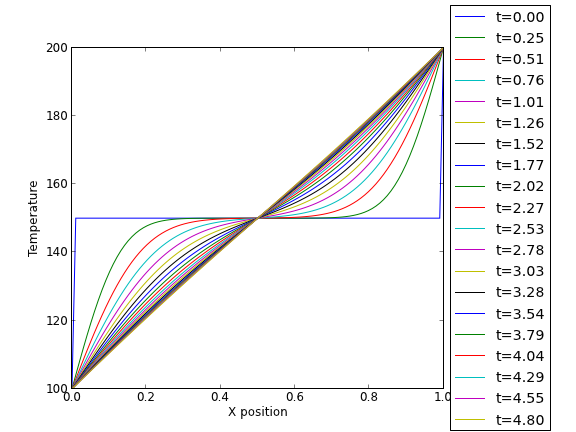
We solved a steady state BVP modeling heat conduction. Today we examine the transient behavior of a rod at constant T put between two heat reservoirs at different temperatures, again T1 = 100, and T2 = 200. The rod will start at 150. Over time, we should expect a solution that approaches the steady state solution: a linear temperature profile from one side of the rod to the other.

\(\frac{\partial u}{\partial t} = k \frac{\partial^2 u}{\partial x^2}\)

at \(t=0\), in this example we have \(u_0(x) = 150\) as an initial condition. with boundary conditions \(u(0,t)=100\) and \(u(L,t)=200\).

In Matlab there is the pdepe command. There is not yet a PDE solver in scipy. Instead, we will utilze the method of lines to solve this problem. We discretize the rod into segments, and approximate the second derivative in the spatial dimension as \(\frac{\partial^2 u}{\partial x^2} = (u(x + h) - 2 u(x) + u(x-h))/ h^2\) at each node. This leads to a set of coupled ordinary differential equations that is easy to solve.

Let us say the rod has a length of 1, \(k=0.02\), and solve for the time-dependent temperature profiles.

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

N = 100  # number of points to discretize
L = 1.0
X = np.linspace(0, L, N) # position along the rod
h = L / (N - 1)

k = 0.02

def odefunc(u, t):
    dudt = np.zeros(X.shape)

    dudt[0] = 0 # constant at boundary condition
    dudt[-1] = 0

    # now for the internal nodes
    for i in range(1, N-1):
        dudt[i] = k * (u[i + 1] - 2*u[i] + u[i - 1]) / h**2

    return dudt

init = 150.0 * np.ones(X.shape) # initial temperature
init[0] = 100.0  # one boundary condition
init[-1] = 200.0 # the other boundary condition

tspan = np.linspace(0.0, 5.0, 100)
sol = odeint(odefunc, init, tspan)


for i in range(0, len(tspan), 5):
    plt.plot(X, sol[i], label='t={0:1.2f}'.format(tspan[i]))

# put legend outside the figure
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
plt.xlabel('X position')
plt.ylabel('Temperature')

# adjust figure edges so the legend is in the figure
plt.subplots_adjust(top=0.89, right=0.77)
plt.savefig('images/pde-transient-heat-1.png')


# Make a 3d figure
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

SX, ST = np.meshgrid(X, tspan)
ax.plot_surface(SX, ST, sol, cmap='jet')
ax.set_xlabel('X')
ax.set_ylabel('time')
ax.set_zlabel('T')
ax.view_init(elev=15, azim=-124) # adjust view so it is easy to see
plt.savefig('images/pde-transient-heat-3d.png')

# animated solution. We will use imagemagick for this

# we save each frame as an image, and use the imagemagick convert command to 
# make an animated gif
for i in range(len(tspan)):
    plt.clf()
    plt.plot(X, sol[i])
    plt.xlabel('X')
    plt.ylabel('T(X)')
    plt.title('t = {0}'.format(tspan[i]))
    plt.savefig('___t{0:03d}.png'.format(i))

import commands
print commands.getoutput('convert -quality 100 ___t*.png images/transient_heat.gif')
print commands.getoutput('rm ___t*.png') #remove temp files

This version of the graphical solution is not that easy to read, although with some study you can see the solution evolves from the initial condition which is flat, to the steady state solution which is a linear temperature ramp.

The 3d version may be easier to interpret. The temperature profile starts out flat, and gradually changes to the linear ramp.

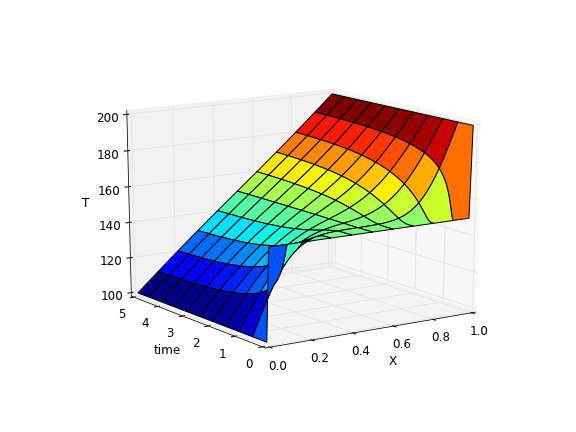
Finally, the animated solution.

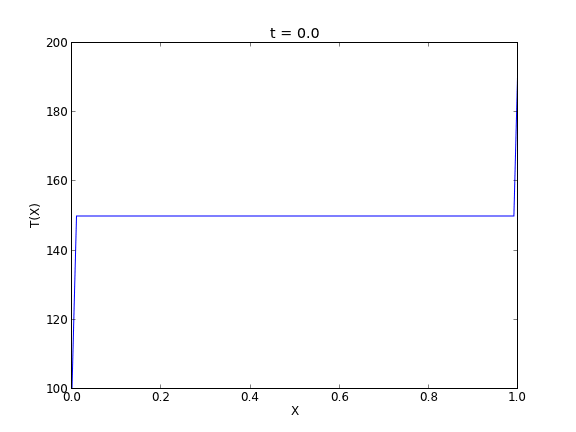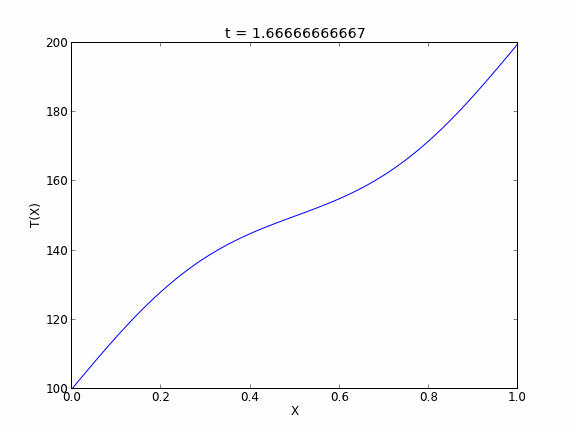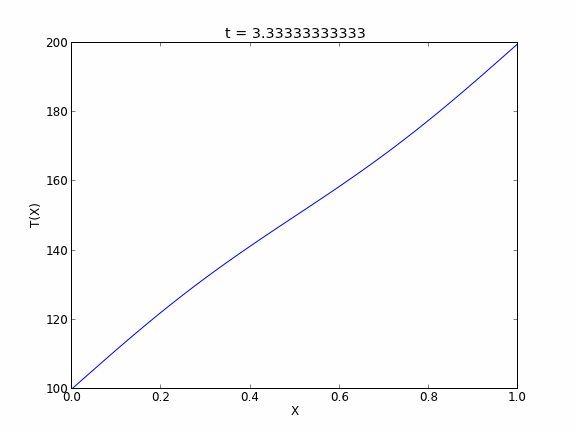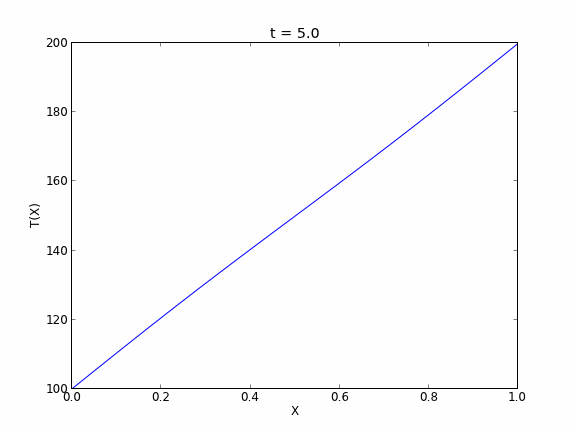
Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source

Matlab post

For steady state heat conduction the temperature distribution in one-dimension is governed by the Laplace equation:

$$ \nabla^2 T = 0$$

with boundary conditions that at \(T(x=a) = T_A\) and \(T(x=L) = T_B\).

The analytical solution is not difficult here: \(T = T_A-\frac{T_A-T_B}{L}x\), but we will solve this by finite differences.

For this problem, lets consider a slab that is defined by x=0 to x=L, with \(T(x=0) = 100\), and \(T(x=L) = 200\). We want to find the function T(x) inside the slab.

We approximate the second derivative by finite differences as

\( f''(x) \approx \frac{f(x-h) - 2 f(x) + f(x+h)}{h^2} \)

Since the second derivative in this case is equal to zero, we have at each discretized node \(0 = T_{i-1} - 2 T_i + T_{i+1}\). We know the values of \(T_{x=0} = \alpha\) and \(T_{x=L} = \beta\).

\[A = \left [ \begin{array}{ccccc} % -2 & 1 & 0 & 0 & 0 \\ 1 & -2& 1 & 0 & 0 \\ 0 & \ddots & \ddots & \ddots & 0 \\ 0 & 0 & 1 & -2 & 1 \\ 0 & 0 & 0 & 1 & -2 \end{array} \right ] \]

\[ x = \left [ \begin{array}{c} T_1 \\ \vdots \\ T_N \end{array} \right ] \]

\[ b = \left [ \begin{array}{c} -T(x=0) \\ 0 \\ \vdots \\ 0 \\ -T(x=L) \end{array} \right] \]

These are linear equations in the unknowns \(x\) that we can easily solve. Here, we evaluate the solution.

import numpy as np

#we use the notation T(x1) = alpha and T(x2) = beta
x1 = 0; alpha = 100
x2 = 5; beta = 200

npoints = 100

# preallocate and shape the b vector and A-matrix
b = np.zeros((npoints, 1));
b[0] = -alpha
b[-1] = -beta

A = np.zeros((npoints, npoints));

#now we populate the A-matrix and b vector elements
for i in range(npoints ):
    for j in range(npoints):
        if j == i: # the diagonal
            A[i,j] = -2
        elif j == i - 1: # left of the diagonal
            A[i,j] = 1
        elif j == i + 1: # right of the diagonal
            A[i,j] = 1
 
# solve the equations A*y = b for Y
Y = np.linalg.solve(A,b)

x = np.linspace(x1, x2, npoints + 2)
y = np.hstack([alpha, Y[:,0], beta])

import matplotlib.pyplot as plt

plt.plot(x, y)

plt.plot(x, alpha + (beta - alpha)/(x2 - x1) * x, 'r--')

plt.xlabel('X')
plt.ylabel('T(X)')
plt.legend(('finite difference', 'analytical soln'), loc='best')
plt.savefig('images/bvp-heat-conduction-1d.png')

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source

There is a heat transfer problem where one needs to find the n^th root of the following equation: \(x J_1(x) - Bi J_0(x)=0\) where \(J_0\) and \(J_1\) are the Bessel functions of zero and first order, and \(Bi\) is the Biot number. We examine an approach to finding these roots.

First, we plot the function.

from scipy.special import jn, jn_zeros
import matplotlib.pyplot as plt
import numpy as np

Bi = 1

def f(x):
    return x * jn(1, x) - Bi * jn(0, x)

X = np.linspace(0, 30, 200)
plt.plot(X, f(X))
plt.savefig('images/heat-transfer-roots-1.png')

You can see there are many roots to this equation, and we want to be sure we get the n^{th} root. This function is pretty well behaved, so if you make a good guess about the solution you will get an answer, but if you make a bad guess, you may get the wrong root. We examine next a way to do it without guessing the solution. What we want is the solution to \(f(x) = 0\), but we want all the solutions in a given interval. We derive a new equation, \(f'(x) = 0\), with initial condition \(f(0) = f0\), and integrate the ODE with an event function that identifies all zeros of \(f\) for us. The derivative of our function is \(df/dx = d/dx(x J_1(x)) - Bi J'_0(x)\). It is known (http://www.markrobrien.com/besselfunct.pdf) that \(d/dx(x J_1(x)) = x J_0(x)\), and \(J'_0(x) = -J_1(x)\). All we have to do now is set up the problem and run it.

from pycse import *  # contains the ode integrator with events

from scipy.special import jn, jn_zeros
import matplotlib.pyplot as plt
import numpy as np

Bi = 1

def f(x):
    "function we want roots for"
    return x * jn(1, x) - Bi * jn(0, x)

def fprime(f, x):
    "df/dx"
    return x * jn(0, x) - Bi * (-jn(1, x))

def e1(f, x):
    "event function to find zeros of f"
    isterminal = False
    value = f
    direction = 0
    return value, isterminal, direction

f0 = f(0)
xspan = np.linspace(0, 30, 200)

x, fsol, XE, FE, IE = odelay(fprime, f0, xspan, events=[e1])

plt.plot(x, fsol, '.-', label='Numerical solution')
plt.plot(xspan, f(xspan), '--', label='Analytical function')
plt.plot(XE, FE, 'ro', label='roots')
plt.legend(loc='best')
plt.savefig('images/heat-transfer-roots-2.png')

for i, root in enumerate(XE):
    print 'root {0} is at {1}'.format(i, root)

plt.show()

root 0 is at 1.25578377377
root 1 is at 4.07947743741
root 2 is at 7.15579904465
root 3 is at 10.2709851256
root 4 is at 13.3983973869
root 5 is at 16.5311587137
root 6 is at 19.6667276775
root 7 is at 22.8039503455
root 8 is at 25.9422288192
root 9 is at 29.081221492

You can work this out once, and then you have all the roots in the interval and you can select the one you want.

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source