Transient heat conduction - partial differential equations
Posted March 07, 2013 at 03:54 PM | categories: pde | tags: heat transfer
Updated March 07, 2013 at 04:25 PM
Matlab post adapated from http://msemac.redwoods.edu/~darnold/math55/DEproj/sp02/AbeRichards/slideshowdefinal.pdf
We solved a steady state BVP modeling heat conduction. Today we examine the transient behavior of a rod at constant T put between two heat reservoirs at different temperatures, again T1 = 100, and T2 = 200. The rod will start at 150. Over time, we should expect a solution that approaches the steady state solution: a linear temperature profile from one side of the rod to the other.
\(\frac{\partial u}{\partial t} = k \frac{\partial^2 u}{\partial x^2}\)
at \(t=0\), in this example we have \(u_0(x) = 150\) as an initial condition. with boundary conditions \(u(0,t)=100\) and \(u(L,t)=200\).
In Matlab there is the pdepe command. There is not yet a PDE solver in scipy. Instead, we will utilze the method of lines to solve this problem. We discretize the rod into segments, and approximate the second derivative in the spatial dimension as \(\frac{\partial^2 u}{\partial x^2} = (u(x + h) - 2 u(x) + u(x-h))/ h^2\) at each node. This leads to a set of coupled ordinary differential equations that is easy to solve.
Let us say the rod has a length of 1, \(k=0.02\), and solve for the time-dependent temperature profiles.
import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt N = 100 # number of points to discretize L = 1.0 X = np.linspace(0, L, N) # position along the rod h = L / (N - 1) k = 0.02 def odefunc(u, t): dudt = np.zeros(X.shape) dudt[0] = 0 # constant at boundary condition dudt[-1] = 0 # now for the internal nodes for i in range(1, N-1): dudt[i] = k * (u[i + 1] - 2*u[i] + u[i - 1]) / h**2 return dudt init = 150.0 * np.ones(X.shape) # initial temperature init[0] = 100.0 # one boundary condition init[-1] = 200.0 # the other boundary condition tspan = np.linspace(0.0, 5.0, 100) sol = odeint(odefunc, init, tspan) for i in range(0, len(tspan), 5): plt.plot(X, sol[i], label='t={0:1.2f}'.format(tspan[i])) # put legend outside the figure plt.legend(loc='center left', bbox_to_anchor=(1, 0.5)) plt.xlabel('X position') plt.ylabel('Temperature') # adjust figure edges so the legend is in the figure plt.subplots_adjust(top=0.89, right=0.77) plt.savefig('images/pde-transient-heat-1.png') # Make a 3d figure from mpl_toolkits.mplot3d import Axes3D fig = plt.figure() ax = fig.add_subplot(111, projection='3d') SX, ST = np.meshgrid(X, tspan) ax.plot_surface(SX, ST, sol, cmap='jet') ax.set_xlabel('X') ax.set_ylabel('time') ax.set_zlabel('T') ax.view_init(elev=15, azim=-124) # adjust view so it is easy to see plt.savefig('images/pde-transient-heat-3d.png') # animated solution. We will use imagemagick for this # we save each frame as an image, and use the imagemagick convert command to # make an animated gif for i in range(len(tspan)): plt.clf() plt.plot(X, sol[i]) plt.xlabel('X') plt.ylabel('T(X)') plt.title('t = {0}'.format(tspan[i])) plt.savefig('___t{0:03d}.png'.format(i)) import commands print commands.getoutput('convert -quality 100 ___t*.png images/transient_heat.gif') print commands.getoutput('rm ___t*.png') #remove temp files
This version of the graphical solution is not that easy to read, although with some study you can see the solution evolves from the initial condition which is flat, to the steady state solution which is a linear temperature ramp.
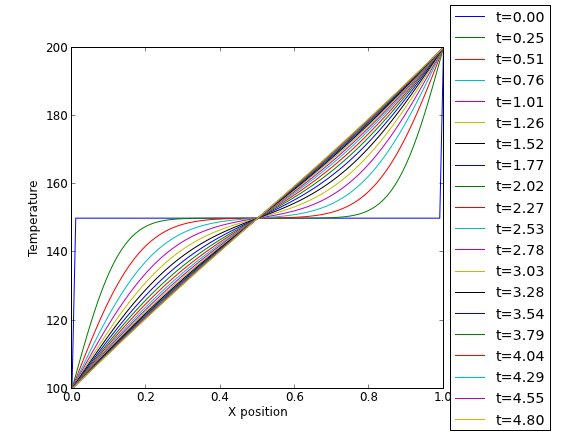
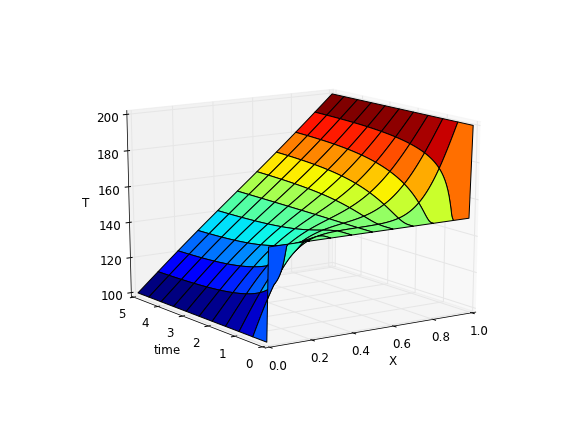
The 3d version may be easier to interpret. The temperature profile starts out flat, and gradually changes to the linear ramp.
Finally, the animated solution.
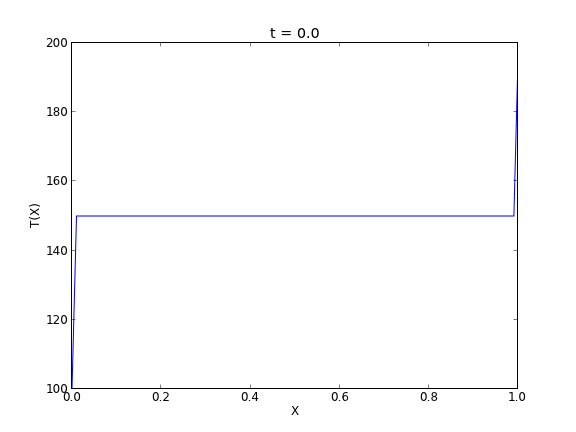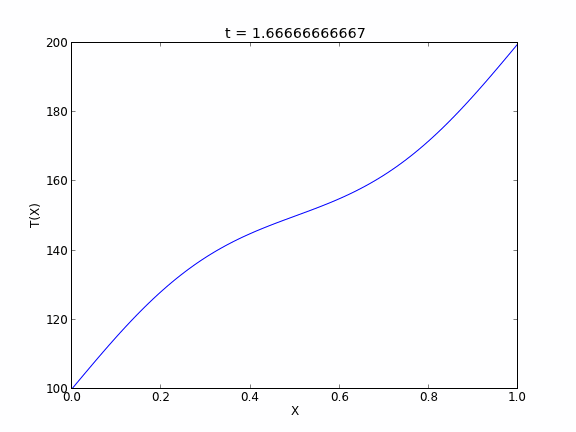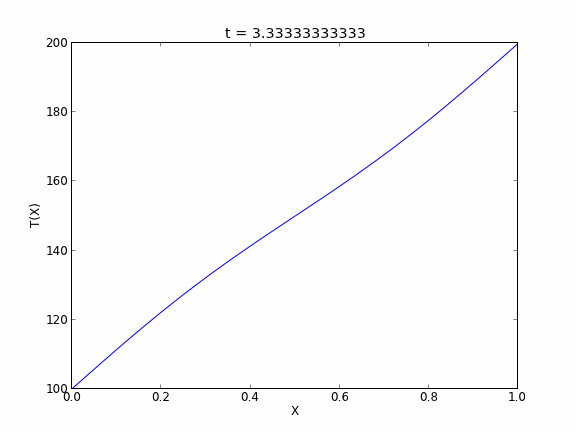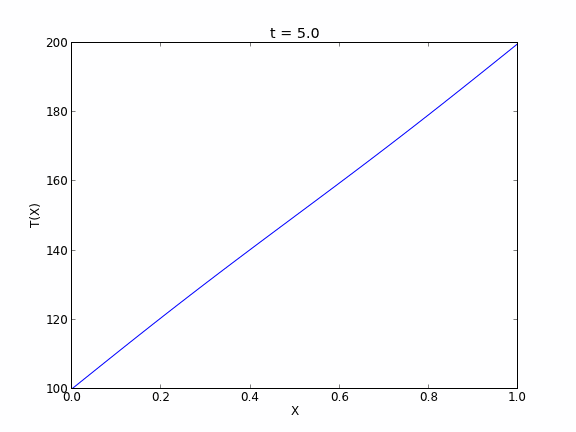
Copyright (C) 2013 by John Kitchin. See the License for information about copying.