The Kitchin Research Group

from pycse import odelay
import matplotlib.pyplot as plt
import numpy as np

def ode(Y,x):
    y1, y2 = Y
    dy1dx = y2
    dy2dx = -y1
    return [dy1dx, dy2dx]

def event1(Y, x):
    y1, y2 = Y
    value = y2 - (-1.0)
    isterminal = True
    direction  = 0
    return value, isterminal, direction

def event2(Y, x):
    dy1dx, dy2dx = ode(Y,x)
    value = dy1dx - 0.0
    isterminal = False
    direction = -1  # derivative is decreasing towards a maximum
    return value, isterminal, direction

Y0 = [2.0, 1.0]
xspan = np.linspace(0, 5)
X, Y, XE, YE, IE = odelay(ode, Y0, xspan, events=[event1, event2])

plt.plot(X, Y)
for ie,xe,ye in zip(IE, XE, YE):
    if ie == 1: #this is the second event
        y1,y2 = ye
        plt.plot(xe, y1, 'ro') 
        
plt.legend(['$y_1$', '$y_2$'], loc='best')
plt.savefig('images/odelay-mult-eq.png')
plt.show()

import quantities as u

k = 0.23 / u.s
Ca0 = 1 * u.mol / u.L

def dCadt(Ca, t):
    return -k * Ca

import numpy as np
from scipy.integrate import odeint

tspan = np.linspace(0, 5) * u.s

sol = odeint(dCadt, Ca0, tspan)

print sol[-1]

import quantities as u
import matplotlib.pyplot as plt

import numpy as np
from scipy.integrate import odeint as _odeint

def odeint(func, y0, t, args=(),
           Dfun=None, col_deriv=0, full_output=0,
           ml=None, mu=None, rtol=None, atol=None,
           tcrit=None, h0=0.0, hmax=0.0, hmin=0.0,
           ixpr=0, mxstep=0, mxhnil=0, mxordn=12,
           mxords=5, printmessg=0):

    def wrapped_func(Y0, T, *args):
        # put units on T if they are on the original t
        # check for units so we don't put them on twice
        if not hasattr(T, 'units') and hasattr(t, 'units'):
            T = T * t.units
        # now for the dependent variable units. Y0 may be a scalar or
        # a list or an array. we want to check each element of y0 for
        # units, and add them to the corresponding element of Y0 if we
        # need to.
        try:
            uY0 = [x for x in Y0] # a list copy of contents of Y0
            # this works if y0 is an iterable, eg. a list or array
            for i, yi in enumerate(y0):
                if not hasattr(uY0[i],'units') and hasattr(yi, 'units'):
               
                    uY0[i] = uY0[i] * yi.units
                
        except TypeError:
            # we have a scalar
            if not hasattr(Y0, 'units') and hasattr(y0, 'units'):
                uY0 = Y0 * y0.units
       
        val = func(uY0, t, *args)

        try:
            return np.array([float(x) for x in val])
        except TypeError:
            return float(val)
    
    if full_output:
        y, infodict = _odeint(wrapped_func, y0, t, args,
                              Dfun, col_deriv, full_output,
                              ml, mu, rtol, atol,
                              tcrit, h0, hmax, hmin,
                              ixpr, mxstep, mxhnil, mxordn,
                              mxords, printmessg)
    else:
        y = _odeint(wrapped_func, y0, t, args,
                    Dfun, col_deriv, full_output,
                    ml, mu, rtol, atol,
                    tcrit, h0, hmax, hmin,
                    ixpr, mxstep, mxhnil, mxordn,
                    mxords, printmessg)

    # now we need to put units onto the solution units should be the
    # same as y0. We cannot put mixed units in an array, so, we return a list
    m,n = y.shape # y is an ndarray, so it has a shape
    if n > 1: # more than one equation, we need a list
        uY = [0 for yi in range(n)]
        
        for i, yi in enumerate(y0):
            if not hasattr(uY[i],'units') and hasattr(yi, 'units'):
                uY[i] = y[:,i] * yi.units
            else:
                uY[i] = y[:,i]
                
    else:
        uY = y * y0.units

    y = uY


    if full_output:
        return y, infodict
    else:
        return y

##################################################################
# test a single ODE
k = 0.23 / u.s
Ca0 = 1 * u.mol / u.L

def dCadt(Ca, t):
    return -k * Ca

tspan = np.linspace(0, 5) * u.s
sol = odeint(dCadt, Ca0, tspan)

print sol[-1]

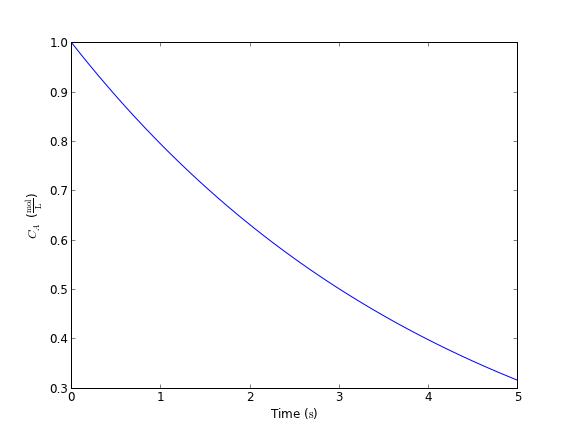
plt.plot(tspan, sol)
plt.xlabel('Time ({0})'.format(tspan.dimensionality.latex))
plt.ylabel('$C_A$ ({0})'.format(sol.dimensionality.latex))
plt.savefig('images/ode-units-ca.png')

##################################################################
# test coupled ODEs
lbmol = 453.59237*u.mol

kprime = 0.0266 * lbmol / u.hr / u.lb
Fa0 = 1.08 * lbmol / u.hr
alpha = 0.0166 / u.lb
epsilon = -0.15

def dFdW(F, W, alpha0):
    X, y = F
    dXdW = kprime / Fa0 * (1.0 - X)/(1.0 + epsilon * X) * y
    dydW = - alpha0 * (1.0 + epsilon * X) / (2.0 * y)
    return [dXdW, dydW]

X0 = 0.0 * u.dimensionless
y0 = 1.0

# initial conditions
F0 = [X0, y0] # one without units, one with units, both are dimensionless

wspan = np.linspace(0,60) * u.lb

sol = odeint(dFdW, F0, wspan, args=(alpha,))
X, y = sol

print 'Test 2'
print X[-1]
print y[-1]

plt.figure()
plt.plot(wspan, X, wspan, y)
plt.legend(['X','$P/P_0$'])
plt.xlabel('Catalyst weight ({0})'.format(wspan.dimensionality.latex))
plt.savefig('images/ode-coupled-units-pdrpo.png')