The Kitchin Research Group

Suppose we have a parameter that has two different values depending on the value of a dimensionless number. For example when the dimensionless number is much less than 1, x = 2/3, and when x is much greater than 1, x = 1. We desire a smooth transition from 2/3 to 1 as a function of x to avoid discontinuities in functions of x. We will adapt the smooth transitions between functions to be a smooth transition between constants.

We define our function as \(x(D) = x0 + (x1 - x0)*(1 - sigma(D,w)\). We control the rate of the transition by the variable \(w\)

import numpy as np
import matplotlib.pyplot as plt

x0 = 2.0 / 3.0
x1 = 1.5

w = 0.05

D = np.linspace(0,2, 500)

sigmaD = 1.0 / (1.0 + np.exp(-(1 - D) / w))

x =  x0 + (x1 - x0)*(1 - sigmaD)

plt.plot(D, x)
plt.xlabel('D'); plt.ylabel('x')
plt.savefig('images/smooth-transitions-constants.png')

This is a nice trick to get an analytical function with continuous derivatives for a transition between two constants. You could have the transition occur at a value other than D = 1, as well by changing the argument to the exponential function.

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source

Matlab post

Adapted from http://biomedicalcomputationreview.org/2/3/8.pdf and http://dl.acm.org/citation.cfm?id=838250.838251

This posts introduces a novel way to numerically estimate the derivative of a function that does not involve finite difference schemes. Finite difference schemes are approximations to derivatives that become more and more accurate as the step size goes to zero, except that as the step size approaches the limits of machine accuracy, new errors can appear in the approximated results. In the references above, a new way to compute the derivative is presented that does not rely on differences!

The new way is: \(f'(x) = \rm{imag}(f(x + i\Delta x)/\Delta x)\) where the function \(f\) is evaluated in imaginary space with a small \(\Delta x\) in the complex plane. The derivative is miraculously equal to the imaginary part of the result in the limit of \(\Delta x \rightarrow 0\)!

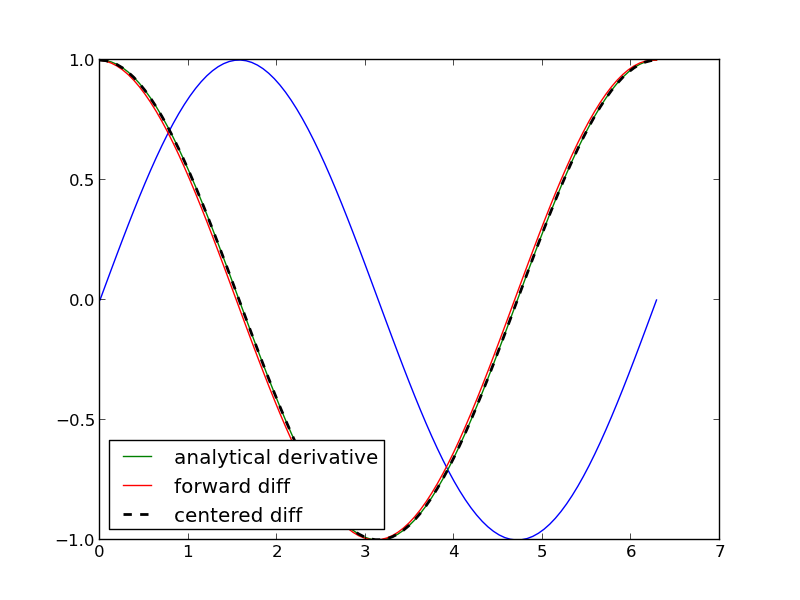
This example comes from the first link. The derivative must be evaluated using the chain rule. We compare a forward difference, central difference and complex-step derivative approximations.

import numpy as np
import matplotlib.pyplot as plt

def f(x):   return np.sin(3*x)*np.log(x)

x = 0.7
h = 1e-7

# analytical derivative
dfdx_a = 3 * np.cos( 3*x)*np.log(x) + np.sin(3*x) / x

# finite difference
dfdx_fd = (f(x + h) - f(x))/h

# central difference
dfdx_cd = (f(x+h)-f(x-h))/(2*h)

# complex method
dfdx_I = np.imag(f(x + np.complex(0, h))/h)

print dfdx_a
print dfdx_fd
print dfdx_cd
print dfdx_cd

1.77335410624
1.7733539398
1.77335410523
1.77335410523

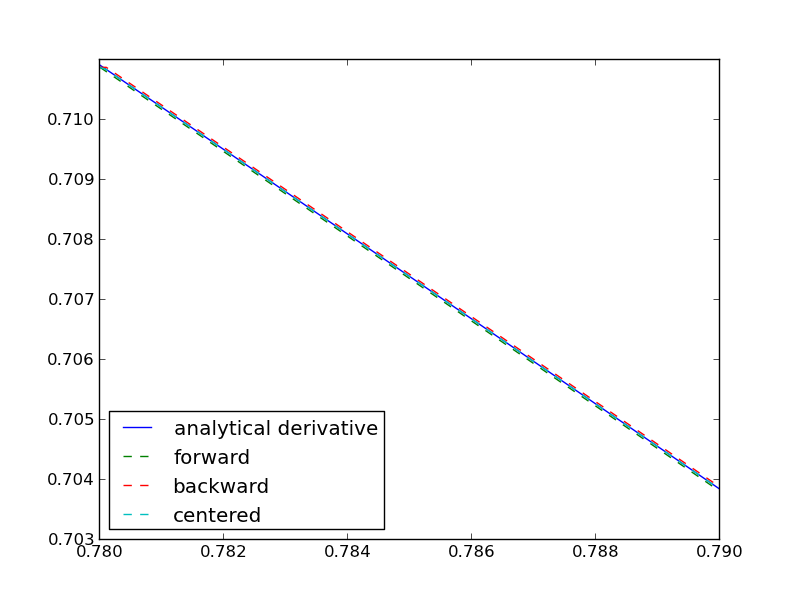
These are all the same to 4 decimal places. The simple finite difference is the least accurate, and the central differences is practically the same as the complex number approach.

Let us use this method to verify the fundamental Theorem of Calculus, i.e. to evaluate the derivative of an integral function. Let \(f(x) = \int\limits_1^{x^2} tan(t^3)dt\), and we now want to compute df/dx. Of course, this can be done analytically, but it is not trivial!

import numpy as np
from scipy.integrate import quad

def f_(z):
    def integrand(t):
        return np.tan(t**3)
    return quad(integrand, 0, z**2)

f = np.vectorize(f_)

x = np.linspace(0, 1)

h = 1e-7

dfdx = np.imag(f(x + complex(0, h)))/h
dfdx_analytical = 2 * x * np.tan(x**6)

import matplotlib.pyplot as plt

plt.plot(x, dfdx, x, dfdx_analytical, 'r--')
plt.show()

>>> >>> ... ... ... ... >>> >>> >>> >>> >>> >>> >>> c:\Python27\lib\site-packages\scipy\integrate\quadpack.py:312: ComplexWarning: Casting complex values to real discards the imaginary part
  return _quadpack._qagse(func,a,b,args,full_output,epsabs,epsrel,limit)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "c:\Python27\lib\site-packages\numpy\lib\function_base.py", line 1885, in __call__
    for x, c in zip(self.ufunc(*newargs), self.otypes)])
  File "<stdin>", line 4, in f_
  File "c:\Python27\lib\site-packages\scipy\integrate\quadpack.py", line 247, in quad
    retval = _quad(func,a,b,args,full_output,epsabs,epsrel,limit,points)
  File "c:\Python27\lib\site-packages\scipy\integrate\quadpack.py", line 312, in _quad
    return _quadpack._qagse(func,a,b,args,full_output,epsabs,epsrel,limit)
TypeError: can't convert complex to float
>>> >>> >>> >>> Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
NameError: name 'dfdx' is not defined

Interesting this fails.

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source

Loops are usually not great for performance. Numpy offers some vectorized methods that allow us to compute derivatives without loops, although this comes at the mental cost of harder to understand syntax

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, 2 * np.pi, 100)
y = np.sin(x)
dy_analytical = np.cos(x)


# we need to specify the size of dy ahead because diff returns
#an array of n-1 elements
dy = np.zeros(y.shape, np.float) #we know it will be this size
dy[0:-1] = np.diff(y) / np.diff(x)
dy[-1] = (y[-1] - y[-2]) / (x[-1] - x[-2])


'''
calculate dy by center differencing using array slices
'''

dy2 = np.zeros(y.shape,np.float) #we know it will be this size
dy2[1:-1] = (y[2:] - y[0:-2]) / (x[2:] - x[0:-2])

# now the end points
dy2[0] = (y[1] - y[0]) / (x[1] - x[0])
dy2[-1] = (y[-1] - y[-2]) / (x[-1] - x[-2])

plt.plot(x,y)
plt.plot(x,dy_analytical,label='analytical derivative')
plt.plot(x,dy,label='forward diff')
plt.plot(x,dy2,'k--',lw=2,label='centered diff')
plt.legend(loc='lower left')
plt.savefig('images/vectorized-diffs.png')
plt.show()

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source

numpy has a function called numpy.diff() that is similar to the one found in matlab. It calculates the differences between the elements in your list, and returns a list that is one element shorter, which makes it unsuitable for plotting the derivative of a function.

Loops in python are pretty slow (relatively speaking) but they are usually trivial to understand. In this script we show some simple ways to construct derivative vectors using loops. It is implied in these formulas that the data points are equally spaced. If they are not evenly spaced, you need a different approach.

import numpy as np
from pylab import *
import time

'''
These are the brainless way to calculate numerical derivatives. They
work well for very smooth data. they are surprisingly fast even up to
10000 points in the vector.
'''

x = np.linspace(0.78,0.79,100)
y = np.sin(x)
dy_analytical = np.cos(x)
'''
lets use a forward difference method:
that works up until the last point, where there is not
a forward difference to use. there, we use a backward difference.
'''

tf1 = time.time()
dyf = [0.0]*len(x)
for i in range(len(y)-1):
    dyf[i] = (y[i+1] - y[i])/(x[i+1]-x[i])
#set last element by backwards difference
dyf[-1] = (y[-1] - y[-2])/(x[-1] - x[-2])

print ' Forward difference took %1.1f seconds' % (time.time() - tf1)

'''and now a backwards difference'''
tb1 = time.time()
dyb = [0.0]*len(x)
#set first element by forward difference
dyb[0] = (y[0] - y[1])/(x[0] - x[1])
for i in range(1,len(y)):
    dyb[i] = (y[i] - y[i-1])/(x[i]-x[i-1])

print ' Backward difference took %1.1f seconds' % (time.time() - tb1)

'''and now, a centered formula'''
tc1 = time.time()
dyc = [0.0]*len(x)
dyc[0] = (y[0] - y[1])/(x[0] - x[1])
for i in range(1,len(y)-1):
    dyc[i] = (y[i+1] - y[i-1])/(x[i+1]-x[i-1])
dyc[-1] = (y[-1] - y[-2])/(x[-1] - x[-2])

print ' Centered difference took %1.1f seconds' % (time.time() - tc1)

'''
the centered formula is the most accurate formula here
'''

plt.plot(x,dy_analytical,label='analytical derivative')
plt.plot(x,dyf,'--',label='forward')
plt.plot(x,dyb,'--',label='backward')
plt.plot(x,dyc,'--',label='centered')

plt.legend(loc='lower left')
plt.savefig('images/simple-diffs.png')
plt.show()

Forward difference took 0.0 seconds
Backward difference took 0.0 seconds
Centered difference took 0.0 seconds

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source

Python is a basic calculator out of the box. Here we consider the most basic mathematical operations: addition, subtraction, multiplication, division and exponenetiation. we use the to get the output. For now we consider integers and float numbers. An integer is a plain number like 0, 10 or -2345. A float number has a decimal in it. The following are all floats: 1.0, -9., and 3.56. Note the trailing zero is not required, although it is good style.

print 2 + 4
print 8.1 - 5

6
3.1

Multiplication is equally straightforward.

print 5 * 4
print 3.1*2

20
6.2

Division is almost as straightforward, but we have to remember that integer division is not the same as float division. Let us consider float division first.

print 4.0 / 2.0
print 1.0/3.1

2.0
0.322580645161

Now, consider the integer versions:

print 4 / 2
print 1/3

2
0

The first result is probably what you expected, but the second may come as a surprise. In integer division the remainder is discarded, and the result is an integer.

Exponentiation is also a basic math operation that python supports directly.

print 3.**2
print 3**2
print 2**0.5

9.0
9
1.41421356237

Other types of mathematical operations require us to import functionality from python libraries. We consider those in the next section.

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source