Vectorized numeric derivatives
Posted February 27, 2013 at 02:51 PM | categories: math | tags:
Updated March 06, 2013 at 06:26 PM
Loops are usually not great for performance. Numpy offers some vectorized methods that allow us to compute derivatives without loops, although this comes at the mental cost of harder to understand syntax
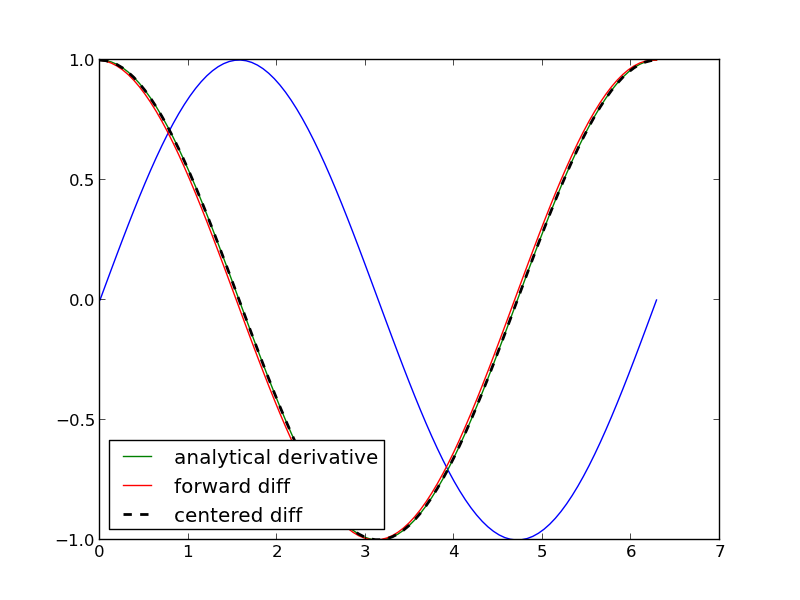
import numpy as np import matplotlib.pyplot as plt x = np.linspace(0, 2 * np.pi, 100) y = np.sin(x) dy_analytical = np.cos(x) # we need to specify the size of dy ahead because diff returns #an array of n-1 elements dy = np.zeros(y.shape, np.float) #we know it will be this size dy[0:-1] = np.diff(y) / np.diff(x) dy[-1] = (y[-1] - y[-2]) / (x[-1] - x[-2]) ''' calculate dy by center differencing using array slices ''' dy2 = np.zeros(y.shape,np.float) #we know it will be this size dy2[1:-1] = (y[2:] - y[0:-2]) / (x[2:] - x[0:-2]) # now the end points dy2[0] = (y[1] - y[0]) / (x[1] - x[0]) dy2[-1] = (y[-1] - y[-2]) / (x[-1] - x[-2]) plt.plot(x,y) plt.plot(x,dy_analytical,label='analytical derivative') plt.plot(x,dy,label='forward diff') plt.plot(x,dy2,'k--',lw=2,label='centered diff') plt.legend(loc='lower left') plt.savefig('images/vectorized-diffs.png') plt.show()
Copyright (C) 2013 by John Kitchin. See the License for information about copying.