Update on finding the minimum distance from a point to a curve
Posted February 17, 2023 at 06:41 PM | categories: optimization | tags:
Almost 10 years ago I wrote about finding the minimum distance from a point to a curve using a constrained optimization. At that time, the way to do this used scipy.optimize.fmin_coblya. I learned today from a student, that sometimes this method fails! I reproduce the code here, updated for Python 3, some style updates, and to show it does indeed fail sometimes, notably when the point is "outside" the parabola.
import numpy as np import matplotlib.pyplot as plt from scipy.optimize import fmin_cobyla def f(x): return x**2 for P in np.array([[0.5, 2], [2, 2], [-1, 2], [-2, 2], [0, 0.5], [0, -0.5]]): def objective(X): X = np.array(X) return np.linalg.norm(X - P) def c1(X): x,y = X return f(x) - y X = fmin_cobyla(objective, x0=[P[0], f(P[0])], cons=[c1]) print(f'The minimum distance is {objective(X):1.2f}. Constraint satisfied = {c1(X) < 1e-6}') # Verify the vector to this point is normal to the tangent of the curve # position vector from curve to point v1 = np.array(P) - np.array(X) # position vector v2 = np.array([1, 2.0 * X[0]]) print('dot(v1, v2) = ', np.dot(v1, v2)) x = np.linspace(-2, 2, 100) plt.plot(x, f(x), 'r-', label='f(x)') plt.plot(P[0], P[1], 'bo', label='point') plt.plot([P[0], X[0]], [P[1], X[1]], 'b-', label='shortest distance') plt.plot([X[0], X[0] + 1], [X[1], X[1] + 2.0 * X[0]], 'g-', label='tangent') plt.axis('equal') plt.xlabel('x') plt.ylabel('y')
The minimum distance is 0.86. Constraint satisfied = True
dot(v1, v2) = 0.0002913487659186309
The minimum distance is 0.00. Constraint satisfied = False
dot(v1, v2) = 0.00021460906432962284
The minimum distance is 0.39. Constraint satisfied = True
dot(v1, v2) = 0.00014271520451364372
The minimum distance is 0.00. Constraint satisfied = False
dot(v1, v2) = -0.0004089466778209598
The minimum distance is 0.50. Constraint satisfied = True
dot(v1, v2) = 1.9999998429305957e-12
The minimum distance is 0.00. Constraint satisfied = False
dot(v1, v2) = 8.588744170160093e-06
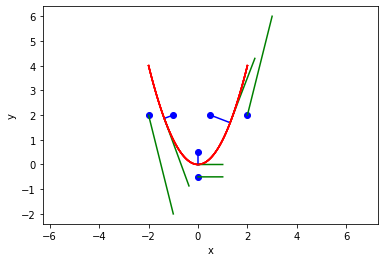
So, sure enough, the optimizer is failing to find a solution that meets the constraint. It is strange it does not work on the outside. That is almost certainly an algorithm problem. Here we solve it nearly identically with the more modern scipy.optimize.minimize function, and it converges every time.
from scipy.optimize import minimize for P in np.array([[0.5, 2], [2, 2], [-1, 2], [-2, 2], [0, 0.5], [0, -0.5]]): def objective(X): X = np.array(X) return np.linalg.norm(X - P) def c1(X): x,y = X return f(x) - y sol = minimize(objective, x0=[P[0], f(P[0])], constraints={'type': 'eq', 'fun': c1}) X = sol.x print(f'The minimum distance is {objective(X):1.2f}. Constraint satisfied = {sol.status < 1e-6}') # Verify the vector to this point is normal to the tangent of the curve # position vector from curve to point v1 = np.array(P) - np.array(X) # position vector v2 = np.array([1, 2.0 * X[0]]) print('dot(v1, v2) = ', np.dot(v1, v2)) x = np.linspace(-2, 2, 100) plt.plot(x, f(x), 'r-', label='f(x)') plt.plot(P[0], P[1], 'bo', label='point') plt.plot([P[0], X[0]], [P[1], X[1]], 'b-', label='shortest distance') plt.plot([X[0], X[0] + 1], [X[1], X[1] + 2.0 * X[0]], 'g-', label='tangent') plt.axis('equal') plt.xlabel('x') plt.ylabel('y')
The minimum distance is 0.86. Constraint satisfied = True
dot(v1, v2) = 1.0701251773603815e-08
The minimum distance is 0.55. Constraint satisfied = True
dot(v1, v2) = -0.0005793028003104883
The minimum distance is 0.39. Constraint satisfied = True
dot(v1, v2) = -1.869272921939391e-05
The minimum distance is 0.55. Constraint satisfied = True
dot(v1, v2) = 0.0005792953298950909
The minimum distance is 0.50. Constraint satisfied = True
dot(v1, v2) = 0.0
The minimum distance is 0.50. Constraint satisfied = True
dot(v1, v2) = 0.0
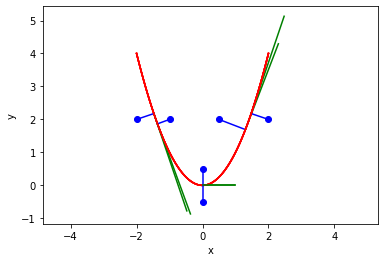
There is no wisdom in fixing the first problem, here I just tried a newer optimization method. Out of the box with default settings it just worked. I did learn the answer is sensitive to the initial guess, so it could make sense to sample the function and find the point that is closest as the initial guess, but here the simple heuristic guess I used worked fine.
Copyright (C) 2023 by John Kitchin. See the License for information about copying.
Org-mode version = 9.5.5