Plane poiseuelle flow solved by finite difference
Posted February 14, 2013 at 09:00 AM | categories: bvp | tags: fluids
Updated March 06, 2013 at 06:32 PM
Adapted from http://www.physics.arizona.edu/~restrepo/475B/Notes/sourcehtml/node24.html
We want to solve a linear boundary value problem of the form: y'' = p(x)y' + q(x)y + r(x) with boundary conditions y(x1) = alpha and y(x2) = beta.
For this example, we solve the plane poiseuille flow problem using a finite difference approach. An advantage of the approach we use here is we do not have to rewrite the second order ODE as a set of coupled first order ODEs, nor do we have to provide guesses for the solution. We do, however, have to discretize the derivatives and formulate a linear algebra problem.
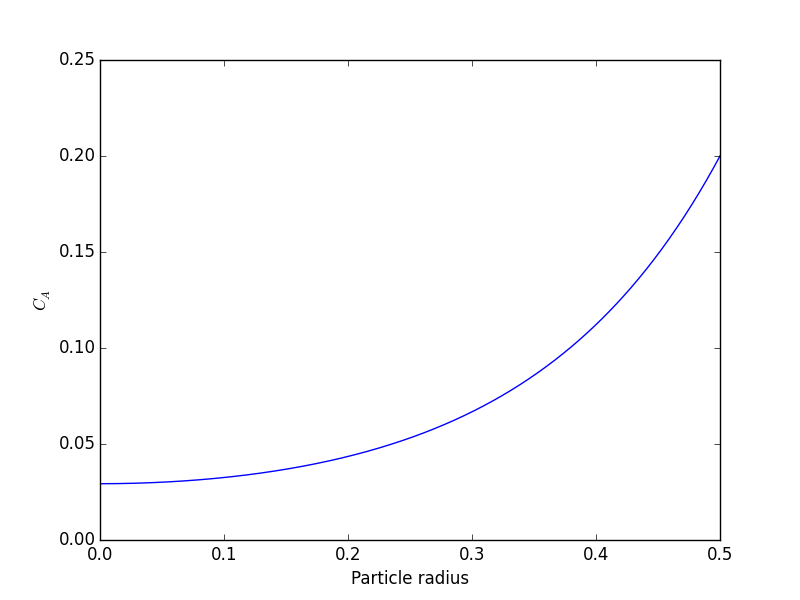
we want to solve u'' = 1/mu*DPDX with u(0)=0 and u(0.1)=0. for this problem we let the plate separation be d=0.1, the viscosity \(\mu = 1\), and \(\frac{\Delta P}{\Delta x} = -100\).
The idea behind the finite difference method is to approximate the derivatives by finite differences on a grid. See here for details. By discretizing the ODE, we arrive at a set of linear algebra equations of the form \(A y = b\), where \(A\) and \(b\) are defined as follows.
\[A = \left [ \begin{array}{ccccc} % 2 + h^2 q_1 & -1 + \frac{h}{2} p_1 & 0 & 0 & 0 \\ -1 - \frac{h}{2} p_2 & 2 + h^2 q_2 & -1 + \frac{h}{2} p_2 & 0 & 0 \\ 0 & \ddots & \ddots & \ddots & 0 \\ 0 & 0 & -1 - \frac{h}{2} p_{N-1} & 2 + h^2 q_{N-1} & -1 + \frac{h}{2} p_{N-1} \\ 0 & 0 & 0 & -1 - \frac{h}{2} p_N & 2 + h^2 q_N \end{array} \right ] \]
\[ y = \left [ \begin{array}{c} y_i \\ \vdots \\ y_N \end{array} \right ] \]
\[ b = \left [ \begin{array}{c} -h^2 r_1 + ( 1 + \frac{h}{2} p_1) \alpha \\ -h^2 r_2 \\ \vdots \\ -h^2 r_{N-1} \\ -h^2 r_N + (1 - \frac{h}{2} p_N) \beta \end{array} \right] \]
import numpy as np # we use the notation for y'' = p(x)y' + q(x)y + r(x) def p(x): return 0 def q(x): return 0 def r(x): return -100 #we use the notation y(x1) = alpha and y(x2) = beta x1 = 0; alpha = 0.0 x2 = 0.1; beta = 0.0 npoints = 100 # compute interval width h = (x2-x1)/npoints; # preallocate and shape the b vector and A-matrix b = np.zeros((npoints - 1, 1)); A = np.zeros((npoints - 1, npoints - 1)); X = np.zeros((npoints - 1, 1)); #now we populate the A-matrix and b vector elements for i in range(npoints - 1): X[i,0] = x1 + (i + 1) * h # get the value of the BVP Odes at this x pi = p(X[i]) qi = q(X[i]) ri = r(X[i]) if i == 0: # first boundary condition b[i] = -h**2 * ri + (1 + h / 2 * pi)*alpha; elif i == npoints - 1: # second boundary condition b[i] = -h**2 * ri + (1 - h / 2 * pi)*beta; else: b[i] = -h**2 * ri # intermediate points for j in range(npoints - 1): if j == i: # the diagonal A[i,j] = 2 + h**2 * qi elif j == i - 1: # left of the diagonal A[i,j] = -1 - h / 2 * pi elif j == i + 1: # right of the diagonal A[i,j] = -1 + h / 2 * pi else: A[i,j] = 0 # off the tri-diagonal # solve the equations A*y = b for Y Y = np.linalg.solve(A,b) x = np.hstack([x1, X[:,0], x2]) y = np.hstack([alpha, Y[:,0], beta]) import matplotlib.pyplot as plt plt.plot(x, y) mu = 1 d = 0.1 x = np.linspace(0,0.1); Pdrop = -100 # this is DeltaP/Deltax u = -(Pdrop) * d**2 / 2.0 / mu * (x / d - (x / d)**2) plt.plot(x,u,'r--') plt.xlabel('distance between plates') plt.ylabel('fluid velocity') plt.legend(('finite difference', 'analytical soln')) plt.savefig('images/pp-bvp-fd.png') plt.show()
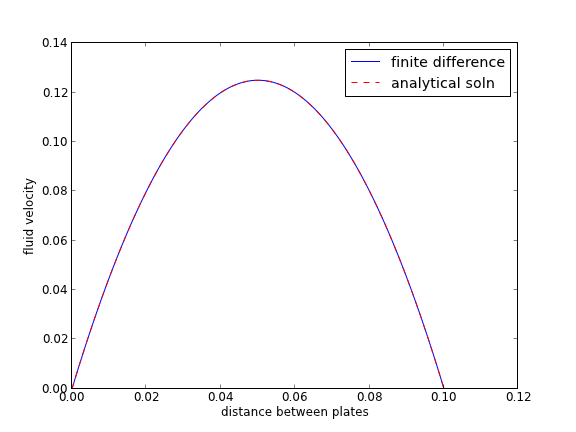
You can see excellent agreement here between the numerical and analytical solution.
Copyright (C) 2013 by John Kitchin. See the License for information about copying.
with boundary conditions 
and 
at 
. We convert this equation to a system of first order ODEs by letting 
. Then, our two equations become:
) at r=0 and Ca(R) = CAs, which makes this a boundary value problem. We use the shooting method here, and guess what Ca(0) is and iterate the guess to get Ca(R) = CAs.
and the derivative of the bottom is 1. So, we have
at 
