The Kitchin Research Group

Matlab post

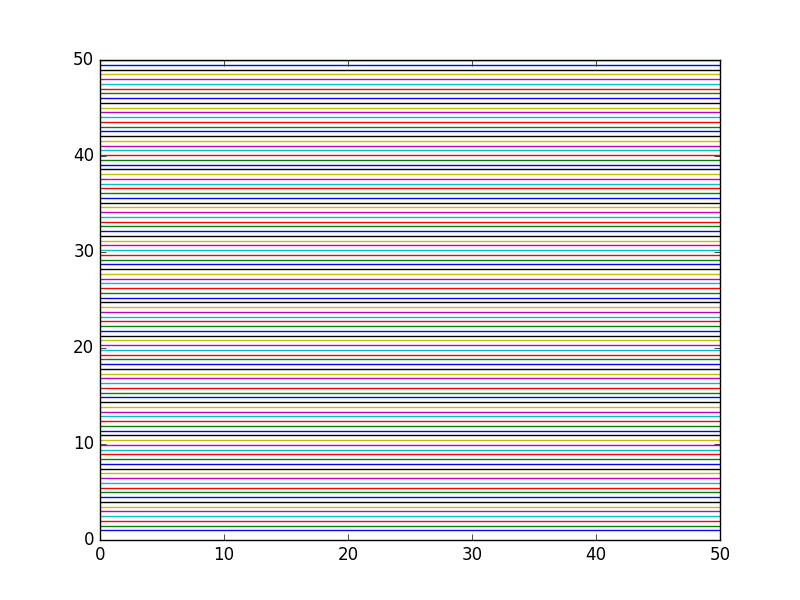
It is an unknown fact that Picasso had a brief blue plotting period with Matlab before moving on to his more famous paintings. It started from irritation with the default colors available in Matlab for plotting. After watching his friend van Gogh cut off his own ear out of frustration with the ugly default colors, Picasso had to do something different.

import numpy as np
import matplotlib.pyplot as plt

#this plots horizontal lines for each y value of m.
for m in np.linspace(1, 50, 100):
    plt.plot([0, 50], [m, m])

plt.savefig('images/blues-1.png')

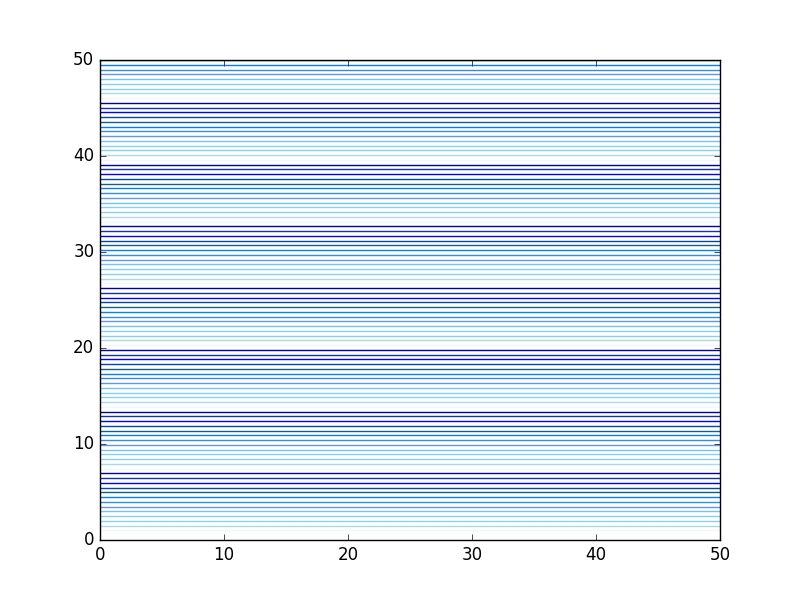
Picasso copied the table available at http://en.wikipedia.org/wiki/List_of_colors and parsed it into a dictionary of hex codes for new colors. That allowed him to specify a list of beautiful blues for his graph. Picasso eventually gave up on python as an artform, and moved on to painting.

import numpy as np
import matplotlib.pyplot as plt

c = {}
with open('color.table') as f:
    for line in f:
        fields = line.split('\t')
        colorname = fields[0].lower()
        hexcode = fields[1]
        c[colorname] = hexcode

names = c.keys()
names = sorted(names)

print(names)

blues = [c['alice blue'],
         c['light blue'],
         c['baby blue'],
         c['light sky blue'],
         c['maya blue'],
         c['cornflower blue'],
         c['bleu de france'],
         c['azure'],
         c['blue sapphire'],
         c['cobalt'],
         c['blue'],
         c['egyptian blue'],
         c['duke blue']]

ax = plt.gca()
ax.set_color_cycle(blues)

#this plots horizontal lines for each y value of m.
for i, m in enumerate(np.linspace(1, 50, 100)):
    plt.plot([0, 50], [m, m])

plt.savefig('images/blues-2.png')

['aero', 'aero blue', 'african violet', 'air force blue (raf)', 'air force blue (usaf)', 'air superiority blue', 'alabama crimson', 'alice blue', 'alizarin crimson', 'alloy orange', 'almond', 'amaranth', 'amazon', 'amber', 'american rose', 'amethyst', 'android green', 'anti-flash white', 'antique brass', 'antique bronze', 'antique fuchsia', 'antique ruby', 'antique white', 'ao (english)', 'apple green', 'apricot', 'aqua', 'aquamarine', 'army green', 'arsenic', 'arylide yellow', 'ash grey', 'asparagus', 'atomic tangerine', 'auburn', 'aureolin', 'aurometalsaurus', 'avocado', 'azure', 'azure mist/web', "b'dazzled blue", 'baby blue', 'baby blue eyes', 'baby pink', 'baby powder', 'baker-miller pink', 'ball blue', 'banana mania', 'banana yellow', 'barbie pink', 'barn red', 'battleship grey', 'bazaar', 'beau blue', 'beaver', 'beige', 'big dip o’ruby', 'bisque', 'bistre', 'bistre brown', 'bitter lemon', 'bitter lime', 'bittersweet', 'bittersweet shimmer', 'black', 'black bean', 'black leather jacket', 'black olive', 'blanched almond', 'blast-off bronze', 'bleu de france', 'blizzard blue', 'blond', 'blue', 'blue (crayola)', 'blue (munsell)', 'blue (ncs)', 'blue (pigment)', 'blue (ryb)', 'blue bell', 'blue sapphire', 'blue yonder', 'blue-gray', 'blue-green', 'blue-violet', 'blueberry', 'bluebonnet', 'blush', 'bole', 'bondi blue', 'bone', 'boston university red', 'bottle green', 'boysenberry', 'brandeis blue', 'brass', 'brick red', 'bright cerulean', 'bright green', 'bright lavender', 'bright maroon', 'bright pink', 'bright turquoise', 'bright ube', 'brilliant lavender', 'brilliant rose', 'brink pink', 'british racing green', 'bronze', 'bronze yellow', 'brown (traditional)', 'brown (web)', 'brown-nose', 'brunswick green', 'bubble gum', 'bubbles', 'buff', 'bulgarian rose', 'burgundy', 'burlywood', 'burnt orange', 'burnt sienna', 'burnt umber', 'byzantine', 'byzantium', 'cadet', 'cadet blue', 'cadet grey', 'cadmium green', 'cadmium orange', 'cadmium red', 'cadmium yellow', 'café au lait', 'café noir', 'cal poly green', 'cambridge blue', 'camel', 'cameo pink', 'camouflage green', 'canary yellow', 'candy apple red', 'candy pink', 'capri', 'caput mortuum', 'cardinal', 'caribbean green', 'carmine', 'carmine (m&p)', 'carmine pink', 'carmine red', 'carnation pink', 'carnelian', 'carolina blue', 'carrot orange', 'castleton green', 'catalina blue', 'catawba', 'cedar chest', 'ceil', 'celadon', 'celadon blue', 'celadon green', 'celeste (colour)', 'celestial blue', 'cerise', 'cerise pink', 'cerulean', 'cerulean blue', 'cerulean frost', 'cg blue', 'cg red', 'chamoisee', 'champagne', 'charcoal', 'charleston green', 'charm pink', 'chartreuse (traditional)', 'chartreuse (web)', 'cherry', 'cherry blossom pink', 'chestnut', 'china pink', 'china rose', 'chinese red', 'chinese violet', 'chocolate (traditional)', 'chocolate (web)', 'chrome yellow', 'cinereous', 'cinnabar', 'cinnamon', 'citrine', 'citron', 'claret', 'classic rose', 'cobalt', 'cocoa brown', 'coconut', 'coffee', 'columbia blue', 'congo pink', 'cool black', 'cool grey', 'copper', 'copper (crayola)', 'copper penny', 'copper red', 'copper rose', 'coquelicot', 'coral', 'coral pink', 'coral red', 'cordovan', 'corn', 'cornell red', 'cornflower blue', 'cornsilk', 'cosmic latte', 'cotton candy', 'cream', 'crimson', 'crimson glory', 'cyan', 'cyan (process)', 'cyber grape', 'cyber yellow', 'daffodil', 'dandelion', 'dark blue', 'dark blue-gray', 'dark brown', 'dark byzantium', 'dark candy apple red', 'dark cerulean', 'dark chestnut', 'dark coral', 'dark cyan', 'dark electric blue', 'dark goldenrod', 'dark gray', 'dark green', 'dark imperial blue', 'dark jungle green', 'dark khaki', 'dark lava', 'dark lavender', 'dark liver', 'dark liver (horses)', 'dark magenta', 'dark midnight blue', 'dark moss green', 'dark olive green', 'dark orange', 'dark orchid', 'dark pastel blue', 'dark pastel green', 'dark pastel purple', 'dark pastel red', 'dark pink', 'dark powder blue', 'dark raspberry', 'dark red', 'dark salmon', 'dark scarlet', 'dark sea green', 'dark sienna', 'dark sky blue', 'dark slate blue', 'dark slate gray', 'dark spring green', 'dark tan', 'dark tangerine', 'dark taupe', 'dark terra cotta', 'dark turquoise', 'dark vanilla', 'dark violet', 'dark yellow', 'dartmouth green', "davy's grey", 'debian red', 'deep carmine', 'deep carmine pink', 'deep carrot orange', 'deep cerise', 'deep champagne', 'deep chestnut', 'deep coffee', 'deep fuchsia', 'deep jungle green', 'deep lemon', 'deep lilac', 'deep magenta', 'deep mauve', 'deep moss green', 'deep peach', 'deep pink', 'deep ruby', 'deep saffron', 'deep sky blue', 'deep space sparkle', 'deep taupe', 'deep tuscan red', 'deer', 'denim', 'desert', 'desert sand', 'diamond', 'dim gray', 'dirt', 'dodger blue', 'dogwood rose', 'dollar bill', 'donkey brown', 'drab', 'duke blue', 'dust storm', 'earth yellow', 'ebony', 'ecru', 'eggplant', 'eggshell', 'egyptian blue', 'electric blue', 'electric crimson', 'electric cyan', 'electric green', 'electric indigo', 'electric lavender', 'electric lime', 'electric purple', 'electric ultramarine', 'electric violet', 'electric yellow', 'emerald', 'english green', 'english lavender', 'english red', 'english violet', 'eton blue', 'eucalyptus', 'fallow', 'falu red', 'fandango', 'fandango pink', 'fashion fuchsia', 'fawn', 'feldgrau', 'feldspar', 'fern green', 'ferrari red', 'field drab', 'fire engine red', 'firebrick', 'flame', 'flamingo pink', 'flattery', 'flavescent', 'flax', 'flirt', 'floral white', 'fluorescent orange', 'fluorescent pink', 'fluorescent yellow', 'folly', 'forest green (traditional)', 'forest green (web)', 'french beige', 'french bistre', 'french blue', 'french lilac', 'french lime', 'french mauve', 'french raspberry', 'french rose', 'french sky blue', 'french wine', 'fresh air', 'fuchsia', 'fuchsia (crayola)', 'fuchsia pink', 'fuchsia rose', 'fulvous', 'fuzzy wuzzy', 'gainsboro', 'gamboge', 'ghost white', 'giants orange', 'ginger', 'glaucous', 'glitter', 'go green', 'gold (metallic)', 'gold (web) (golden)', 'gold fusion', 'golden brown', 'golden poppy', 'golden yellow', 'goldenrod', 'granny smith apple', 'grape', 'gray', 'gray (html/css gray)', 'gray (x11 gray)', 'gray-asparagus', 'gray-blue', 'green (color wheel) (x11 green)', 'green (crayola)', 'green (html/css color)', 'green (munsell)', 'green (ncs)', 'green (pigment)', 'green (ryb)', 'green-yellow', 'grullo', 'guppie green', 'halayà úbe', 'han blue', 'han purple', 'hansa yellow', 'harlequin', 'harvard crimson', 'harvest gold', 'heart gold', 'heliotrope', 'hollywood cerise', 'honeydew', 'honolulu blue', "hooker's green", 'hot magenta', 'hot pink', 'hunter green', 'iceberg', 'icterine', 'illuminating emerald', 'imperial', 'imperial blue', 'imperial purple', 'imperial red', 'inchworm', 'india green', 'indian red', 'indian yellow', 'indigo', 'indigo (dye)', 'indigo (web)', 'international klein blue', 'international orange (aerospace)', 'international orange (engineering)', 'international orange (golden gate bridge)', 'iris', 'irresistible', 'isabelline', 'islamic green', 'italian sky blue', 'ivory', 'jade', 'japanese indigo', 'japanese violet', 'jasmine', 'jasper', 'jazzberry jam', 'jelly bean', 'jet', 'jonquil', 'june bud', 'jungle green', 'kelly green', 'kenyan copper', 'keppel', 'khaki (html/css) (khaki)', 'khaki (x11) (light khaki)', 'kobe', 'kobi', 'ku crimson', 'la salle green', 'languid lavender', 'lapis lazuli', 'laser lemon', 'laurel green', 'lava', 'lavender (floral)', 'lavender (web)', 'lavender blue', 'lavender blush', 'lavender gray', 'lavender indigo', 'lavender magenta', 'lavender mist', 'lavender pink', 'lavender purple', 'lavender rose', 'lawn green', 'lemon', 'lemon chiffon', 'lemon curry', 'lemon glacier', 'lemon lime', 'lemon meringue', 'lemon yellow', 'licorice', 'light apricot', 'light blue', 'light brown', 'light carmine pink', 'light coral', 'light cornflower blue', 'light crimson', 'light cyan', 'light fuchsia pink', 'light goldenrod yellow', 'light gray', 'light green', 'light khaki', 'light medium orchid', 'light moss green', 'light orchid', 'light pastel purple', 'light pink', 'light red ochre', 'light salmon', 'light salmon pink', 'light sea green', 'light sky blue', 'light slate gray', 'light steel blue', 'light taupe', 'light thulian pink', 'light yellow', 'lilac', 'lime (color wheel)', 'lime (web) (x11 green)', 'lime green', 'limerick', 'lincoln green', 'linen', 'lion', 'little boy blue', 'liver', 'liver (dogs)', 'liver (organ)', 'liver chestnut', 'lumber', 'lust', 'magenta', 'magenta (crayola)', 'magenta (dye)', 'magenta (pantone)', 'magenta (process)', 'magic mint', 'magnolia', 'mahogany', 'maize', 'majorelle blue', 'malachite', 'manatee', 'mango tango', 'mantis', 'mardi gras', 'maroon (crayola)', 'maroon (html/css)', 'maroon (x11)', 'mauve', 'mauve taupe', 'mauvelous', 'maya blue', 'meat brown', 'medium aquamarine', 'medium blue', 'medium candy apple red', 'medium carmine', 'medium champagne', 'medium electric blue', 'medium jungle green', 'medium lavender magenta', 'medium orchid', 'medium persian blue', 'medium purple', 'medium red-violet', 'medium ruby', 'medium sea green', 'medium sky blue', 'medium slate blue', 'medium spring bud', 'medium spring green', 'medium taupe', 'medium turquoise', 'medium tuscan red', 'medium vermilion', 'medium violet-red', 'mellow apricot', 'mellow yellow', 'melon', 'metallic seaweed', 'metallic sunburst', 'mexican pink', 'midnight blue', 'midnight green (eagle green)', 'midori', 'mikado yellow', 'mint', 'mint cream', 'mint green', 'misty rose', 'moccasin', 'mode beige', 'moonstone blue', 'mordant red 19', 'moss green', 'mountain meadow', 'mountbatten pink', 'msu green', 'mughal green', 'mulberry', 'mustard', 'myrtle green', 'sae/ece amber (color)']

Copyright (C) 2018 by John Kitchin. See the License for information about copying.

org-mode source

Org-mode version = 9.1.6

Matlab post

This example shows how to use a regular expression to find strings matching the pattern :cmd:`datastring`. We want to find these strings, and then replace them with something that depends on what cmd is, and what datastring is.

Let us define some commands that will take datasring as an argument, and return the modified text. The idea is to find all the cmds, and then run them. We use python's eval command to get the function handle from a string, and the cmd functions all take a datastring argument (we define them that way). We will create commands to replace :cmd:`datastring` with html code for a light gray background, and :red:`some text` with html code making the text red.

text = r'''Here is some text. use the :cmd:`open` to get the text into
          a variable. It might also be possible to get a multiline
            :red:`line     
     2` directive.'''

print text
print '---------------------------------'

... ... >>> >>> Here is some text. use the :cmd:`open` to get the text into
          a variable. It might also be possible to get a multiline
            :red:`line     
     2` directive.
---------------------------------

Now, we define our functions.

def cmd(datastring):
    ' replace :cmd:`datastring` with html code with light gray background'
    s = '<FONT style="BACKGROUND-COLOR: LightGray">%{0}</FONT>';
    html = s.format(datastring)
    return html

def red(datastring):
    'replace :red:`datastring` with html code to make datastring in red font'
    html = '<font color=red>{0}</font>'.format(datastring)
    return html

Finally, we do the regular expression. Regular expressions are hard. There are whole books on them. The point of this post is to alert you to the possibilities. I will break this regexp down as follows. 1. we want everything between :*: as the directive. ([^:]*) matches everything not a :. :([^:]*): matches the stuff between two :. 2. then we want everything between `*`. ([^`]*) matches everything not a `. 3. The () makes a group that python stores so we can refer to them later.

import re
regex = ':([^:]*):`([^`]*)`'
matches = re.findall(regex, text)
for directive, datastring in matches:
    directive = eval(directive) # get the function
    text = re.sub(regex, directive(datastring), text)

print 'Modified text:'
print text

>>> >>> ... ... ... >>> Modified text:
Here is some text. use the <FONT style="BACKGROUND-COLOR: LightGray">%open</FONT> to get the text into
          a variable. It might also be possible to get a multiline
            <FONT style="BACKGROUND-COLOR: LightGray">%open</FONT> directive.

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source

Matlab post Python has capability to do symbolic math through the sympy package.

from sympy import solve, symbols, pprint

a,b,c,x = symbols('a,b,c,x')

f = a*x**2 + b*x + c

solution = solve(f, x)
print solution
pprint(solution)

>>> >>> >>> >>> >>> >>> [(-b + (-4*a*c + b**2)**(1/2))/(2*a), -(b + (-4*a*c + b**2)**(1/2))/(2*a)]
_____________   /       _____________\ 
        /           2    |      /           2 | 
 -b + \/  -4*a*c + b    -\b + \/  -4*a*c + b  / 
[---------------------, -----------------------]
          2*a                     2*a

from sympy import diff

print diff(f, x)
print diff(f, x, 2)

print diff(f, a)

>>> 2*a*x + b
2*a
>>> x**2

from sympy import integrate

print integrate(f, x)          # indefinite integral
print integrate(f, (x, 0, 1))  # definite integral from x=0..1

>>> a*x**3/3 + b*x**2/2 + c*x
a/3 + b/2 + c

from sympy import Function, Symbol, dsolve
f = Function('f')
x = Symbol('x')
fprime = f(x).diff(x) - f(x) # f' = f(x)

y = dsolve(fprime, f(x))

print y
print y.subs(x,4)
print [y.subs(x, X) for X in [0, 0.5, 1]] # multiple values

>>> >>> >>> >>> >>> >>> f(x) == exp(C1 + x)
f(4) == exp(C1 + 4)
[f(0) == exp(C1), f(0.5) == exp(C1 + 0.5), f(1) == exp(C1 + 1)]

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source

Matlab post Yesterday in Post 1324 we looked at a way to solve nonlinear equations that takes away some of the burden of initial guess generation. The idea was to reformulate the equations with a new variable \(\lambda\), so that at \(\lambda=0\) we have a simpler problem we know how to solve, and at \(\lambda=1\) we have the original set of equations. Then, we derive a set of ODEs on how the solution changes with \(\lambda\), and solve them.

Today we look at a simpler example and explain a little more about what is going on. Consider the equation: \(f(x) = x^2 - 5x + 6 = 0\), which has two roots, \(x=2\) and \(x=3\). We will use the method of continuity to solve this equation to illustrate a few ideas. First, we introduce a new variable \(\lambda\) as: \(f(x; \lambda) = 0\). For example, we could write \(f(x;\lambda) = \lambda x^2 - 5x + 6 = 0\). Now, when \(\lambda=0\), we hve the simpler equation \(- 5x + 6 = 0\), with the solution \(x=6/5\). The question now is, how does \(x\) change as \(\lambda\) changes? We get that from the total derivative of how \(f(x,\lambda)\) changes with \(\lambda\). The total derivative is:

$$\frac{df}{d\lambda} = \frac{\partial f}{\partial \lambda} + \frac{\partial f}{\partial x}\frac{\partial x}{\partial \lambda}=0$$

We can calculate two of those quantities: \(\frac{\partial f}{\partial \lambda}\) and \(\frac{\partial f}{\partial x}\) analytically from our equation and solve for \(\frac{\partial x}{\partial \lambda}\) as

$$ \frac{\partial x}{\partial \lambda} = -\frac{\partial f}{\partial \lambda}/\frac{\partial f}{\partial x}$$

That defines an ordinary differential equation that we can solve by integrating from \(\lambda=0\) where we know the solution to \(\lambda=1\) which is the solution to the real problem. For this problem: \(\frac{\partial f}{\partial \lambda}=x^2\) and \(\frac{\partial f}{\partial x}=-5 + 2\lambda x\).

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

def dxdL(x, Lambda):
    return -x**2 / (-5.0 + 2 * Lambda * x)

x0 = 6.0/5.0
Lspan = np.linspace(0, 1)
x = odeint(dxdL, x0, Lspan)

plt.plot(Lspan, x)
plt.xlabel('$\lambda$')
plt.ylabel('x')
plt.savefig('images/nonlin-contin-II-1.png')

We found one solution at x=2. What about the other solution? To get that we have to introduce \(\lambda\) into the equations in another way. We could try: \(f(x;\lambda) = x^2 + \lambda(-5x + 6)\), but this leads to an ODE that is singular at the initial starting point. Another approach is \(f(x;\lambda) = x^2 + 6 + \lambda(-5x)\), but now the solution at \(\lambda=0\) is imaginary, and we do not have a way to integrate that! What we can do instead is add and subtract a number like this: \(f(x;\lambda) = x^2 - 4 + \lambda(-5x + 6 + 4)\). Now at \(\lambda=0\), we have a simple equation with roots at \(\pm 2\), and we already know that \(x=2\) is a solution. So, we create our ODE on \(dx/d\lambda\) with initial condition \(x(0) = -2\).

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

def dxdL(x, Lambda):
    return (5 * x - 10) / (2 * x - 5 * Lambda)

x0 = -2
Lspan = np.linspace(0, 1)
x = odeint(dxdL, x0, Lspan)

plt.plot(Lspan, x)
plt.xlabel('$\lambda$')
plt.ylabel('x')
plt.savefig('images/nonlin-contin-II-2.png')

Now we have the other solution. Note if you choose the other root, \(x=2\), you find that 2 is a root, and learn nothing new. You could choose other values to add, e.g., if you chose to add and subtract 16, then you would find that one starting point leads to one root, and the other starting point leads to the other root. This method does not solve all problems associated with nonlinear root solving, namely, how many roots are there, and which one is “best” or physically reasonable? But it does give a way to solve an equation where you have no idea what an initial guess should be. You can see, however, that just like you can get different answers from different initial guesses, here you can get different answers by setting up the equations differently.

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source

Matlab post Occasionally we have a set of vectors and we need to determine whether the vectors are linearly independent of each other. This may be necessary to determine if the vectors form a basis, or to determine how many independent equations there are, or to determine how many independent reactions there are.

Reference: Kreysig, Advanced Engineering Mathematics, sec. 7.4

Matlab provides a rank command which gives you the number of singular values greater than some tolerance. The numpy.rank function, unfortunately, does not do that. It returns the number of dimensions in the array. We will just compute the rank from singular value decomposition.

The default tolerance used in Matlab is max(size(A))*eps(norm(A)). Let us break that down. eps(norm(A)) is the positive distance from abs(X) to the next larger in magnitude floating point number of the same precision as X. Basically, the smallest significant number. We multiply that by the size of A, and take the largest number. We have to use some judgment in what the tolerance is, and what “zero” means.

import numpy as np
v1 = [6, 0, 3, 1, 4, 2];
v2 = [0, -1, 2, 7, 0, 5];
v3 = [12, 3, 0, -19, 8, -11];

A = np.row_stack([v1, v2, v3])

# matlab definition
eps = np.finfo(np.linalg.norm(A).dtype).eps
TOLERANCE = max(eps * np.array(A.shape))

U, s, V = np.linalg.svd(A)
print s
print np.sum(s > TOLERANCE)

TOLERANCE = 1e-14
print np.sum(s > TOLERANCE)

>>> >>> >>> >>> >>> >>> ... >>> >>> >>> >>> [  2.75209239e+01   9.30584482e+00   1.42425400e-15]
3
>>> >>> 2

You can see if you choose too small a TOLERANCE, nothing looks like zero. the result with TOLERANCE=1e-14 suggests the rows are not linearly independent. Let us show that one row can be expressed as a linear combination of the other rows.

The number of rows is greater than the rank, so these vectors are not independent. Let's demonstrate that one vector can be defined as a linear combination of the other two vectors. Mathematically we represent this as:

\(x_1 \mathit{v1} + x_2 \mathit{v2} = v3\)

or

\([x_1 x_2][v1; v2] = v3\)

This is not the usual linear algebra form of Ax = b. To get there, we transpose each side of the equation to get:

[v1.T v2.T][x_1; x_2] = v3.T

which is the form Ax = b. We solve it in a least-squares sense.

A = np.column_stack([v1, v2])
x = np.linalg.lstsq(A, v3)
print x[0]

>>> [ 2. -3.]

This shows that v3 = 2*v1 - 3*v2

#Problem set 7.4 #17
import numpy as np

v1 = [0.2, 1.2, 5.3, 2.8, 1.6]
v2 = [4.3, 3.4, 0.9, 2.0, -4.3]

A = np.row_stack([v1, v2])
U, s, V = np.linalg.svd(A)
print s

[ 7.57773162  5.99149259]

import numpy as np

A = [[1, 2, 3],
     [0, 2, 3],
     [0, 0, 1e-6]]

U, s, V = np.linalg.svd(A)
print s
print np.sum(np.abs(s) > 1e-15)
print np.sum(np.abs(s) > 1e-5)

[  5.14874857e+00   7.00277208e-01   5.54700196e-07]
3
2

import numpy as np

#    [H2  H Br2 Br HBr]
M = [[-1,  0, -1,  0,  2],  # H2 + Br2 == 2HBR
     [ 0,  0, -1,  2,  0],  # Br2 == 2Br
     [-1,  1,  0, -1,  1],  # Br + H2 == HBr + H
     [ 0, -1, -1,  1,  1],  # H + Br2 == HBr + Br
     [ 1, -1,  0,  1,  -1], # H + HBr == H2 + Br
     [ 0,  0,  1, -2,  0]]  # 2Br == Br2

U, s, V = np.linalg.svd(M)
print s
print np.sum(np.abs(s) > 1e-15)

import sympy 
M = sympy.Matrix(M)
reduced_form, inds = M.rref()

print reduced_form

labels = ['H2',  'H', 'Br2', 'Br', 'HBr']
for row in reduced_form.tolist():
    s = '0 = '
    for nu,species in zip(row,labels):
        if nu != 0:
            
            s += ' {0:+d}{1}'.format(int(nu), species)
    if s != '0 = ': print s

[  3.84742803e+00   3.32555975e+00   1.46217301e+00   1.73313660e-16
   8.57422679e-17]
3
[1, 0, 0,  2, -2]
[0, 1, 0,  1, -1]
[0, 0, 1, -2,  0]
[0, 0, 0,  0,  0]
[0, 0, 0,  0,  0]
[0, 0, 0,  0,  0]
0 =  +1H2 +2Br -2HBr
0 =  +1H +1Br -1HBr
0 =  +1Br2 -2Br

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source