The Kitchin Research Group

Here is the new syntax with manager.

import numpy as np
from scipy.optimize import minimize

def objective(x):
    return np.exp(x**2) - 10 * np.exp(x)


@check_result
def maxIterationsExceeded(args, sol):
    if sol.message == 'Maximum number of iterations has been exceeded.':
        args['maxiter'] *= 2
        return args

@manager(checkers=[maxIterationsExceeded], verbose=True)
def get_result(maxiter=2):
    return minimize(objective, 0.0, options={'maxiter': maxiter})

get_result(2)

Proposed fix in wrapper: {'maxiter': 4}
Proposed fix in wrapper: {'maxiter': 8}
  message: Optimization terminated successfully.
  success: True
   status: 0
      fun: -36.86307468296428
        x: [ 1.662e+00]
      nit: 5
      jac: [-4.768e-07]
 hess_inv: [[ 6.481e-03]]
     nfev: 26
     njev: 13

It works!

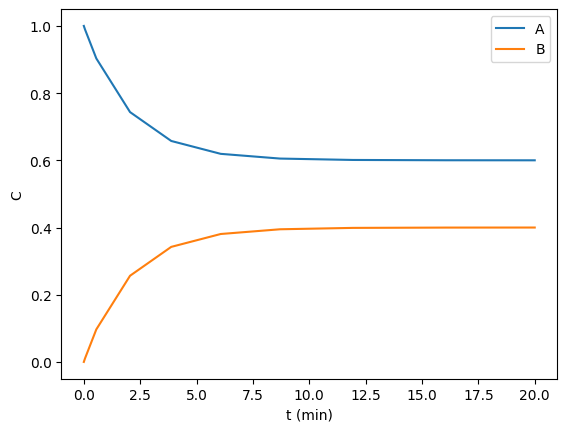
In this example, we aim to find the steady state concentrations of two species by integrating a mass balance to steady state. This is visually easy to see below, the concentrations are essentially flat after 10 min or so. Computationally this is somewhat tricky to find though. A way to do it is to compare some windows of integration to see if the values are not changing very fast. For instance you could average the values from 10 to 11, and compare that to the values in 11 to 12, and keep doing that until they are close enough to the same.

def ode(t, C):
    Ca, Cb = C
    dCadt = -0.2 * Ca + 0.3 * Cb
    dCbdt = -0.3 * Cb + 0.2 * Ca
    return dCadt, dCbdt

tspan = (0, 20)

from scipy.integrate import solve_ivp
sol = solve_ivp(ode, tspan, (1, 0))

import matplotlib.pyplot as plt
plt.plot(sol.t, sol.y.T)
plt.xlabel('t (min)')
plt.ylabel('C')
plt.legend(['A', 'B']);
sol.y.T[-1]

array([0.60003278, 0.39996722])

It is not crucial to use a class here; you could also use global variables, or function attributes. A class is a standard way of encapsulating state though. We just have to make the class callable so it acts like a function when we need it to.

class ReachedSteadyState:        
    def __init__(self, tolerance=0.01):
        self.tolerance = tolerance
        self.last_solution = None
        self.count = 0

    def __str__(self):
        return 'ReachedSteadyState'

    @check_result
    def __call__(self, args, sol):
        if self.last_solution is None:
            self.last_solution = sol
            self.count += 1
            args['C0'] = sol.y.T[-1]
            return args

        # we have a previous solution
        if not np.allclose(self.last_solution.y.mean(axis=1),
                           sol.y.mean(axis=1),
                           rtol=self.tolerance,
                           atol=self.tolerance):
            self.last_solution = sol
            self.count += 1
            args['C0'] = sol.y.T[-1]
            return args

rss = ReachedSteadyState(0.0001)

@manager(checkers=[rss], max_errors=20, verbose=True)        
def get_sol(C0=(1, 0), window=1):
    sol = solve_ivp(ode, t_span=(0, window), y0=C0)
    return sol

sol = get_sol((1, 0), window=2)
sol

Proposed fix in ReachedSteadyState: {'C0': array([0.74716948, 0.25283052]), 'window': 2} Proposed fix in ReachedSteadyState: {'C0': array([0.65414484, 0.34585516]), 'window': 2} Proposed fix in ReachedSteadyState: {'C0': array([0.61992776, 0.38007224]), 'window': 2} Proposed fix in ReachedSteadyState: {'C0': array([0.60733496, 0.39266504]), 'window': 2} Proposed fix in ReachedSteadyState: {'C0': array([0.60269957, 0.39730043]), 'window': 2} Proposed fix in ReachedSteadyState: {'C0': array([0.60099346, 0.39900654]), 'window': 2} Proposed fix in ReachedSteadyState: {'C0': array([0.60036557, 0.39963443]), 'window': 2} Proposed fix in ReachedSteadyState: {'C0': array([0.60013451, 0.39986549]), 'window': 2} Proposed fix in ReachedSteadyState: {'C0': array([0.60004949, 0.39995051]), 'window': 2}

  message: The solver successfully reached the end of the integration interval.
  success: True
   status: 0
        t: [ 0.000e+00  7.179e-01  2.000e+00]
        y: [[ 6.000e-01  6.000e-01  6.000e-01]
            [ 4.000e-01  4.000e-01  4.000e-01]]
      sol: None
 t_events: None
 y_events: None
     nfev: 14
     njev: 0
      nlu: 0

We can plot the two solutions to see how different they are. This shows they are close.

import matplotlib.pyplot as plt
plt.plot(rss.last_solution.t, rss.last_solution.y.T, label=['A previous' ,'B previous'])
plt.plot(sol.t, sol.y.T, '--', label=['A current', 'B current'])
plt.legend()
plt.xlabel('relative t')
plt.ylabel('C');

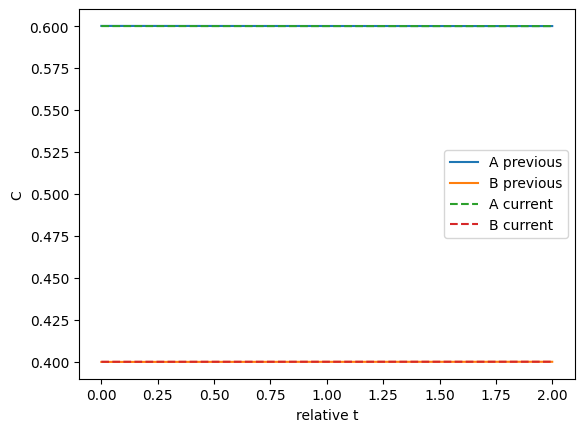
Those look pretty similar on this graph.

Suppose you have a function that randomly fails. This could be because something does not converge with a randomly chosen initial guess, converges to an unphysical answer, etc. In these cases, it makes sense to simply try again with a new initial guess.

For this example, say we have this objective function with two minima. We will say that any solution above 0.5 is unphysical.

def f(x):
    return -(np.exp(-50 * (x - 0.25)**2) + 0.5 * np.exp(-100 * (x - 0.75)**2))


x = np.linspace(0, 1)
plt.plot(x, f(x))
plt.xlabel('x')
plt.ylabel('y');

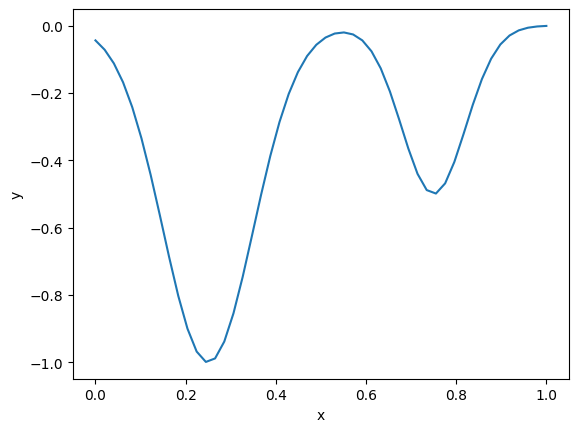
Here we define a function that takes a guess, and gets a solution. If the solution is unphysical, we raise an exception. We define a custom exception so we can handle it specifically.

class UnphysicalSolution(Exception):
    pass

def get_minima(guess):
    sol = minimize(f, guess)

    if sol.x > 0.5:
        raise UnphysicalSolution
    else:
        return sol

@check_exception
def try_again(args, exc):
    if isinstance(exc, UnphysicalSolution):
        args['guess'] = np.random.random()
        return args
  
@manager(checkers=(try_again,), verbose=True)    
def get_minima(guess):
    sol = minimize(f, guess)

    if sol.x > 0.5:
        raise UnphysicalSolution
    else:
        return sol

get_minima(np.random.random())

Proposed fix in wrapper: {'guess': 0.03789731690063758}
  message: Optimization terminated successfully.
  success: True
   status: 0
      fun: -1.0000000000069411
        x: [ 2.500e-01]
      nit: 4
      jac: [ 0.000e+00]
 hess_inv: [[ 1.000e-02]]
     nfev: 18
     njev: 9

You can see it took four iterations to find a solution. Other times it might take zero or one, or maybe more, it depends on where the guesses fall.

This solution works as well as supervisor did. It was a little deeper rabbit hole to go down, mostly because of some subtlety in making the result and exception decorators work for both functions and class methods. I think it is more robust now, as it should not matter how you call the function, and any combination of args and kwargs should be working.