Equation of a plane through three points

Posted January 18, 2015 at 10:48 AM | categories: python | tags:

We are given three points, and we seek the equation of the plane that goes through them. The method is straight forward. A plane is defined by the equation:

\(a x + b y + c z = d\)

and we just need the coefficients. The \(a, b, c\) coefficients are obtained from a vector normal to the plane, and \(d\) is calculated separately. We get the normal vector from the cross-product of two vectors connecting the points, and we get \(d\) from the dot product of the normal vector with any one of the point position vectors.

Finally, given the equation, we want to generate a mesh that samples the plane, and plot the mesh and original points to verify the plane goes through the points. Here is the implementation. 

import numpy as np

p1 = np.array([1, 2, 3])
p2 = np.array([4, 6, 9])
p3 = np.array([12, 11, 9])

# These two vectors are in the plane
v1 = p3 - p1
v2 = p2 - p1

# the cross product is a vector normal to the plane
cp = np.cross(v1, v2)
a, b, c = cp

# This evaluates a * x3 + b * y3 + c * z3 which equals d
d = np.dot(cp, p3)

print('The equation is {0}x + {1}y + {2}z = {3}'.format(a, b, c, d))

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

x = np.linspace(-2, 14, 5)
y = np.linspace(-2, 14, 5)
X, Y = np.meshgrid(x, y)

Z = (d - a * X - b * Y) / c

# plot the mesh. Each array is 2D, so we flatten them to 1D arrays
ax.plot(X.flatten(),
        Y.flatten(),
        Z.flatten(), 'bo ')

# plot the original points. We use zip to get 1D lists of x, y and z
# coordinates.
ax.plot(*zip(p1, p2, p3), color='r', linestyle=' ', marker='o')

# adjust the view so we can see the point/plane alignment
ax.view_init(0, 22)
plt.tight_layout()
plt.savefig('images/plane.png')
plt.show()

The equation is 30x + -48y + 17z = -15

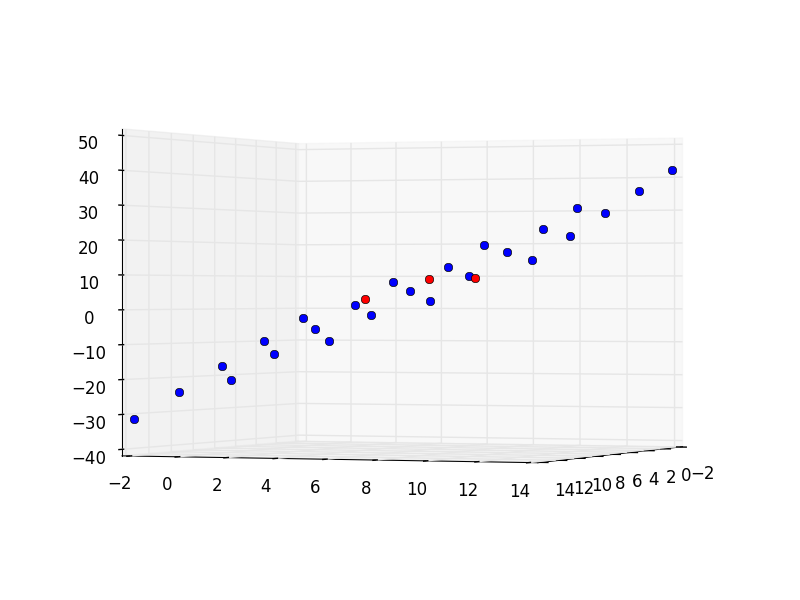It looks like the blue points form a plane that contains the red points.

Copyright (C) 2015 by John Kitchin. See the License for information about copying.

org-mode source

Org-mode version = 8.2.10

Discuss on Twitter