What region is a point in
Posted June 06, 2013 at 10:35 AM | categories: programming | tags:
Updated June 26, 2013 at 06:55 PM
Suppose we have a space that is divided by a boundary into two regions, and we want to know if an arbitrary point is on one region or the other. One way to figure this out is to pick a point that is known to be in a region, and then draw a line to the arbitrary point counting the number of times it crosses the boundary. If the line crosses an even number of times, then the point is in the same region and if it crosses an odd number of times, then the point is in the other region.
Here is the boundary and region we consider in this example:
boundary = [[0.1, 0],
[0.25, 0.1],
[0.3, 0.2],
[0.35, 0.34],
[0.4, 0.43],
[0.51, 0.47],
[0.48, 0.55],
[0.44, 0.62],
[0.5, 0.66],
[0.55,0.57],
[0.556, 0.48],
[0.63, 0.43],
[0.70, 0.44],
[0.8, 0.51],
[0.91, 0.57],
[1.0, 0.6]]
import matplotlib.pyplot as plt
plt.plot([p[0] for p in boundary],
[p[1] for p in boundary])
plt.ylim([0, 1])
plt.savefig('images/boundary-1.png')
... ... ... ... ... ... ... ... ... ... ... ... ... ... >>> >>> >>> >>> >>> ... [<matplotlib.lines.Line2D object at 0x00000000062FEBA8>] (0, 1)
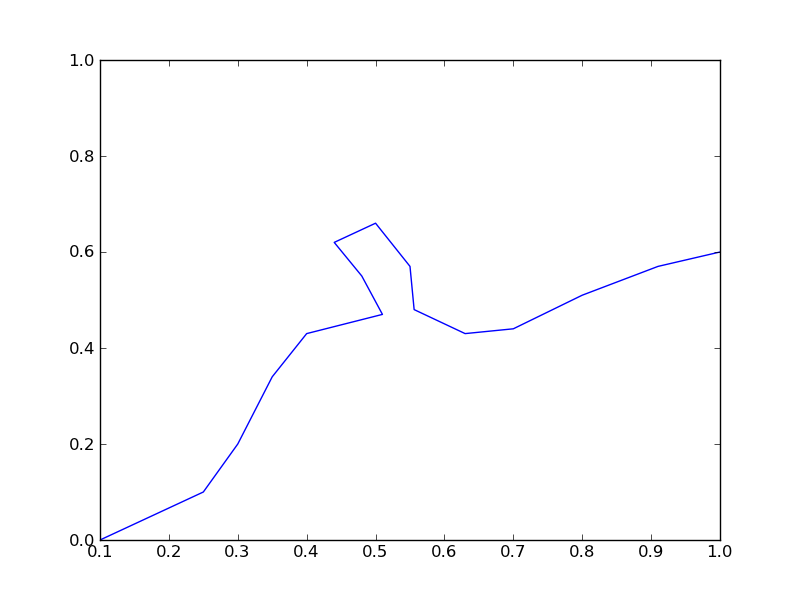
In this example, the boundary is complicated, and not described by a simple function. We will check for intersections of the line from the arbitrary point to the reference point with each segment defining the boundary. If there is an intersection in the boundary, we count that as a crossing. We choose the origin (0, 0) in this case for the reference point. For an arbitrary point (x1, y1), the equation of the line is therefore (provided x1 !=0):
\(y = \frac{y1}{x1} x\).
Let the points defining a boundary segment be (bx1, by1) and (bx2, by2). The equation for the line connecting these points (provided bx1 != bx2) is:
\(y = by1 + \frac{by2 - by1}{bx2 - bx1}(x - bx1)\)
Setting these two equations equal to each other, we can solve for the value of \(x\), and if \(bx1 <= x <= bx2\) then we would say there is an intersection with that segment. The solution for x is:
\(x = \frac{m bx1 - by1}{m - y1/x1}\)
This can only fail if \(m = y1/x1\) which means the segments are parallel and either do not intersect or go through each other. One issue we have to resolve is what to do when the intersection is at the boundary. In that case, we would see an intersection with two segments since bx1 of one segment is also bx2 of another segment. We resolve the issue by only counting intersections with bx1. Finally, there may be intersections at values of \(x\) greater than the point, and we are not interested in those because the intersections are not between the point and reference point.
Here are all of the special cases that we have to handle:
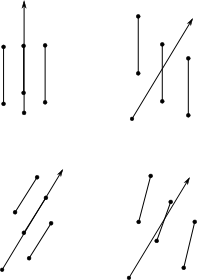
We will have to do float comparisons, so we will define tolerance functions for all of these. I tried this previously with regular comparison operators, and there were many cases that did not work because of float comparisons. In the code that follows, we define the tolerance functions, the function that handles almost all the special cases, and show that it almost always correctly identifies the region a point is in.
import numpy as np TOLERANCE = 2 * np.spacing(1) def feq(x, y, epsilon=TOLERANCE): 'x == y' return not((x < (y - epsilon)) or (y < (x - epsilon))) def flt(x, y, epsilon=TOLERANCE): 'x < y' return x < (y - epsilon) def fgt(x, y, epsilon=TOLERANCE): 'x > y' return y < (x - epsilon) def fle(x, y, epsilon=TOLERANCE): 'x <= y' return not(y < (x - epsilon)) def fge(x, y, epsilon=TOLERANCE): 'x >= y' return not(x < (y - epsilon)) boundary = [[0.1, 0], [0.25, 0.1], [0.3, 0.2], [0.35, 0.34], [0.4, 0.43], [0.51, 0.47], [0.48, 0.55], [0.44, 0.62], [0.5, 0.66], [0.55,0.57], [0.556, 0.48], [0.63, 0.43], [0.70, 0.44], [0.8, 0.51], [0.91, 0.57], [1.0, 0.6]] def intersects(p, isegment): 'p is a point (x1, y1), isegment is an integer indicating which segment starting with 0' x1, y1 = p bx1, by1 = boundary[isegment] bx2, by2 = boundary[isegment + 1] # outline cases to handle if feq(bx1, bx2) and feq(x1, 0.0): # both segments are vertical if feq(bx1, x1): return True else: return False elif feq(bx1, bx2): # segment is vertical m1 = y1 / x1 # slope of reference line y = m1 * bx1 # value of reference line at bx1 if ((fge(y, by1) and flt(y, by2)) or (fle(y, by1) and fgt(y,by2))): # reference line intersects the segment return True else: return False else: # neither reference line nor segment is vertical m = (by2 - by1) / (bx2 - bx1) # segment slope m1 = y1 / x1 if feq(m, m1): # line and segment are parallel if feq(y1, m * bx1): return True else: return False else: # lines are not parallel x = (m * bx1 - by1) / (m - m1) # x at intersection if ((fge(x, bx1) and flt(x, bx2)) or (fle(x, bx1) and fgt(x, bx2))) and fle(x, x1): return True else: return False raise Exception('you should not get here') import matplotlib.pyplot as plt plt.plot([p[0] for p in boundary], [p[1] for p in boundary], 'go-') plt.ylim([0, 1]) N = 100 X = np.linspace(0, 1, N) for x in X: for y in X: p = (x, y) nintersections = sum([intersects(p, i) for i in range(len(boundary) - 1)]) if nintersections % 2 == 0: plt.plot(x, y, 'r.') else: plt.plot(x, y, 'b.') plt.savefig('images/boundary-2.png') plt.show()
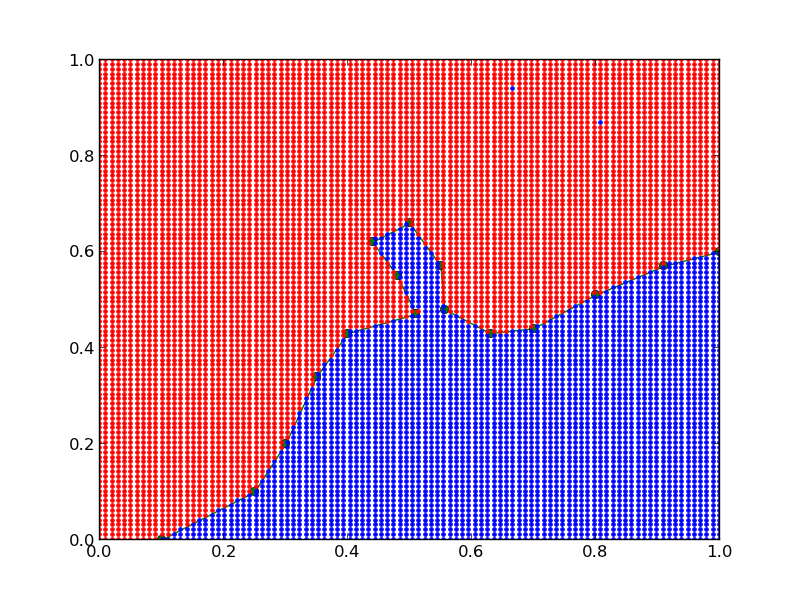
If you look carefully, there are two blue points in the red region, which means there is some edge case we do not capture in our function. Kudos to the person who figures it out.
Copyright (C) 2013 by John Kitchin. See the License for information about copying.