A nonlinear BVP

Posted March 08, 2013 at 09:19 AM | categories: pde | tags:

Adapted from Example 8.7 in _Numerical Methods in Engineering with Python_ by Jaan Kiusalaas.

We want to solve $y''(x) = -3 y(x) y'(x)$ with $y(0) = 0 and $y(2) = 1$ using a finite difference method. We discretize the region and approximate the derivatives as:

$y''(x) \approx \frac{y_{i-1} - 2 y_i + y_{i+1}}{h^2} $

$y'(x) \approx \frac{y_{i+1} - y_{i-1}}{2 h} $

We define a function $y''(x) = F(x, y, y')$. At each node in our discretized region, we will have an equation that looks like $y''(x) - F(x, y, y') = 0$, which will be nonlinear in the unknown solution $y$. The set of equations to solve is:

\begin{eqnarray} y_0 - \alpha &=& 0 \\ \frac{y_{i-1} - 2 y_i + y_{i+1}}{h^2} + (3 y_i) (\frac{y_{i+1} - y_{i-1}}{2 h}) &=& 0 \\ y_L - \beta &=&0 \end{eqnarray}

Since we use a nonlinear solver, we will have to provide an initial guess to the solution. We will in this case assume a line. In other cases, a bad initial guess may lead to no solution.

import numpy as np
from scipy.optimize import fsolve
import matplotlib.pyplot as plt

x1 = 0.0
x2 = 2.0

alpha = 0.0
beta = 1.0

N = 11
X = np.linspace(x1, x2, N)
h = (x2 - x1) / (N - 1)

def Ypp(x, y, yprime):
    '''define y'' = 3*y*y' '''
    return -3.0 * y * yprime

def residuals(y):
    '''When we have the right values of y, this function will be zero.'''

    res = np.zeros(y.shape)

    res[0] = y[0] - alpha
    
    for i in range(1, N - 1):
        x = X[i]
        YPP = (y[i - 1] - 2 * y[i] + y[i + 1]) / h**2
        YP = (y[i + 1] - y[i - 1]) / (2 * h)
        res[i] = YPP - Ypp(x, y[i], YP)

    res[-1] = y[-1] - beta
    return res

# we need an initial guess
init = alpha + (beta - alpha) / (x2 - x1) * X

Y = fsolve(residuals, init)

plt.plot(X, Y)
plt.savefig('images/bvp-nonlinear-1.png')

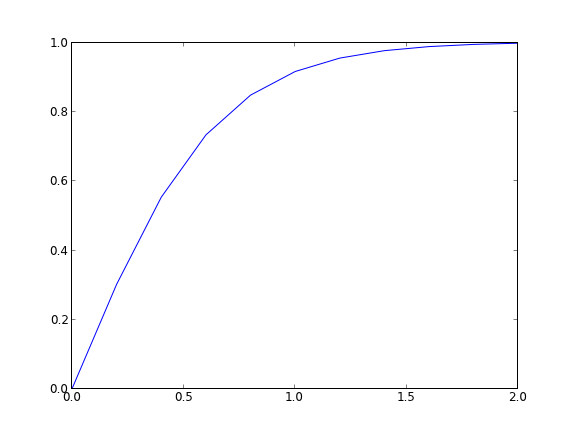
That code looks useful, so I put it in the pycse module in the function BVP_nl. Here is an example usage. We have to create two functions, one for the differential equation, and one for the initial guess.

from pycse import  BVP_nl
import matplotlib.pyplot as plt

def Ypp(x, y, yprime):
    '''define y'' = 3*y*y' '''
    return -3.0 * y * yprime

def init(x):
    return alpha + (beta - alpha) / (x2 - x1) * x

x1 = 0.0
x2 = 2.0

alpha = 0.0
beta = 1.0

N = 11
x, y = BVP_nl(Ypp, x1, x2, alpha, beta, init, N)

plt.plot(x, y)
plt.savefig('images/bvp-nonlinear-2.png')

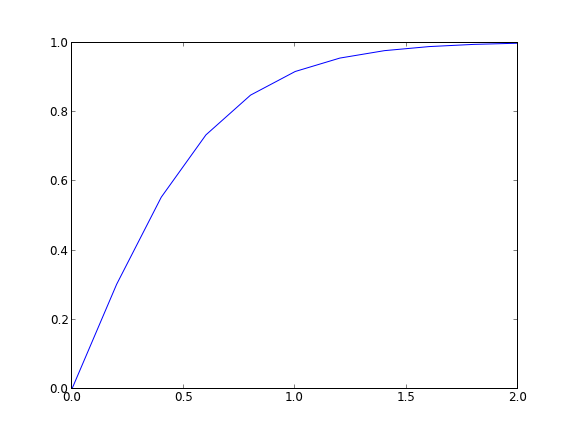
The results are the same.

org-mode source

The Kitchin Research Group

Chemical Engineering at Carnegie Mellon University

A nonlinear BVP