The Kitchin Research Group

Matlab post

import numpy as np
import matplotlib.pyplot as plt

x = np.array([0.0,       1.1,       2.3,      3.1,       4.05,      6.0])
y = np.array([0.0039,    1.2270,    5.7035,   10.6472,   18.6032,   42.3024])

plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.savefig('images/nonlin-minsse-1.png')

>>> >>> >>> >>> >>> [<matplotlib.lines.Line2D object at 0x000000000733D898>]
<matplotlib.text.Text object at 0x00000000071EC5C0>
<matplotlib.text.Text object at 0x00000000071EED30>

We are going to fit the function \(y = x^a\) to the data. The best \(a\) will minimize the summed squared error between the model and the fit.

def errfunc_(a):
    return np.sum((y - x**a)**2)

errfunc = np.vectorize(errfunc_)

arange = np.linspace(1, 3)
sse = errfunc(arange)

plt.figure()
plt.plot(arange, sse)
plt.xlabel('a')
plt.ylabel('$\Sigma (y - y_{pred})^2$')
plt.savefig('images/nonlin-minsse-2.png')

... >>> >>> >>> >>> >>> >>> <matplotlib.figure.Figure object at 0x000000000736DBA8>
[<matplotlib.lines.Line2D object at 0x00000000075CBEF0>]
<matplotlib.text.Text object at 0x00000000076B8C18>
<matplotlib.text.Text object at 0x0000000007698BE0>

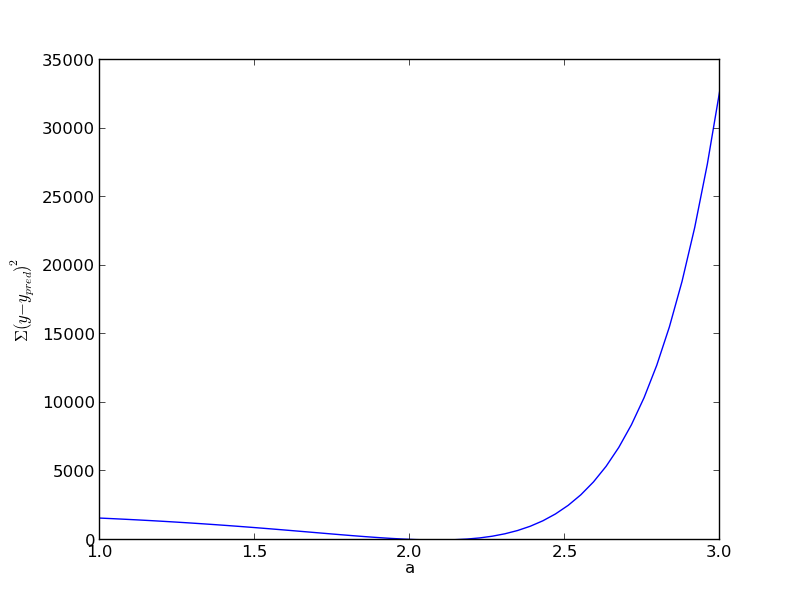
Based on the graph above, you can see a minimum in the summed squared error near \(a = 2.1\). We use that as our initial guess. Since we know the answer is bounded, we use scipy.optimize.fminbound

from scipy.optimize import fminbound

amin = fminbound(errfunc, 1.0, 3.0)

print amin

plt.figure()
plt.plot(x, y, 'bo', label='data')
plt.plot(x, x**amin, 'r-', label='fit')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc='best')
plt.savefig('images/nonlin-minsse-3.png')

>>> >>> >>> 2.09004838933
>>> <matplotlib.figure.Figure object at 0x00000000075D8470>
[<matplotlib.lines.Line2D object at 0x0000000007BDFA20>]
[<matplotlib.lines.Line2D object at 0x0000000007BDFC18>]
<matplotlib.text.Text object at 0x0000000007BC6828>
<matplotlib.text.Text object at 0x0000000007BCAF98>
<matplotlib.legend.Legend object at 0x0000000007BE3128>

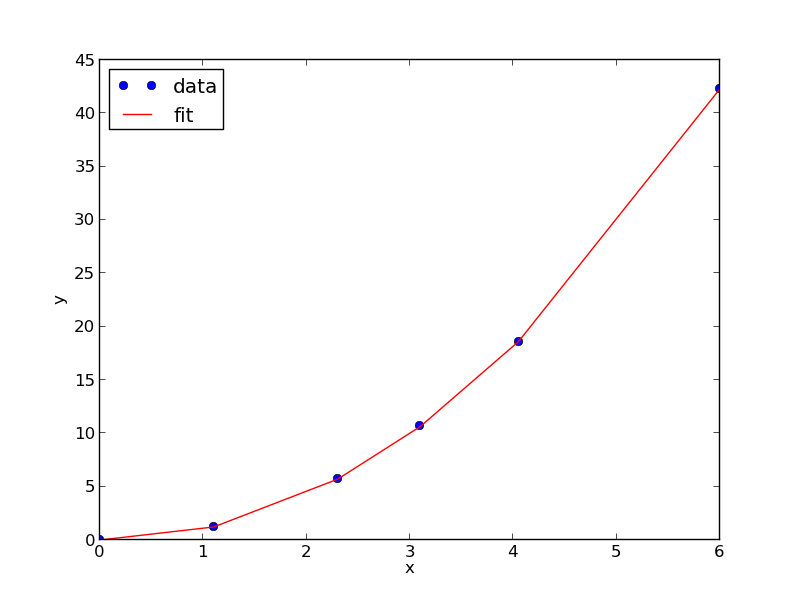
We can do nonlinear fitting by directly minimizing the summed squared error between a model and data. This method lacks some of the features of other methods, notably the simple ability to get the confidence interval. However, this method is flexible and may offer more insight into how the solution depends on the parameters.

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source