Solving Bessel's Equation numerically
Posted February 07, 2013 at 09:00 AM | categories: math, ode | tags:
Updated March 06, 2013 at 06:33 PM
Reference Ch 5.5 Kreysig, Advanced Engineering Mathematics, 9th ed.
Bessel's equation \(x^2 y'' + x y' + (x^2 - \nu^2)y=0\) comes up often in engineering problems such as heat transfer. The solutions to this equation are the Bessel functions. To solve this equation numerically, we must convert it to a system of first order ODEs. This can be done by letting \(z = y'\) and \(z' = y''\) and performing the change of variables:
$$ y' = z$$
$$ z' = \frac{1}{x^2}(-x z - (x^2 - \nu^2) y$$
if we take the case where \(\nu = 0\), the solution is known to be the Bessel function \(J_0(x)\), which is represented in Matlab as besselj(0,x). The initial conditions for this problem are: \(y(0) = 1\) and \(y'(0)=0\).
There is a problem with our system of ODEs at x=0. Because of the \(1/x^2\) term, the ODEs are not defined at x=0. If we start very close to zero instead, we avoid the problem.
import numpy as np from scipy.integrate import odeint from scipy.special import jn # bessel function import matplotlib.pyplot as plt def fbessel(Y, x): nu = 0.0 y = Y[0] z = Y[1] dydx = z dzdx = 1.0 / x**2 * (-x * z - (x**2 - nu**2) * y) return [dydx, dzdx] x0 = 1e-15 y0 = 1 z0 = 0 Y0 = [y0, z0] xspan = np.linspace(1e-15, 10) sol = odeint(fbessel, Y0, xspan) plt.plot(xspan, sol[:,0], label='numerical soln') plt.plot(xspan, jn(0, xspan), 'r--', label='Bessel') plt.legend() plt.savefig('images/bessel.png')
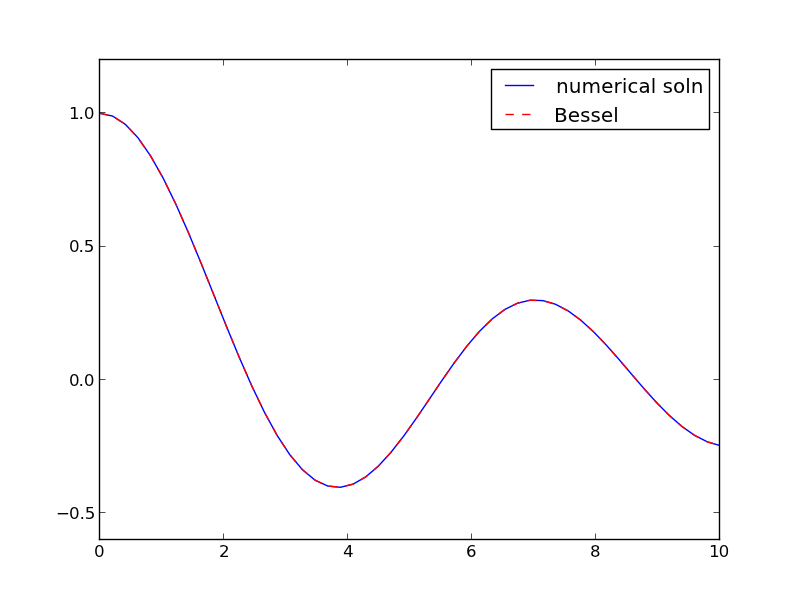
You can see the numerical and analytical solutions overlap, indicating they are at least visually the same.
Copyright (C) 2013 by John Kitchin. See the License for information about copying.