The Kitchin Research Group

Matlab post

The odesolvers in scipy can only solve first order ODEs, or systems of first order ODES. To solve a second order ODE, we must convert it by changes of variables to a system of first order ODES. We consider the Van der Pol oscillator here:

$$\frac{d^2x}{dt^2} - \mu(1-x^2)\frac{dx}{dt} + x = 0$$

\(\mu\) is a constant. If we let \(y=x - x^3/3\) http://en.wikipedia.org/wiki/Van_der_Pol_oscillator, then we arrive at this set of equations:

$$\frac{dx}{dt} = \mu(x-1/3x^3-y)$$

$$\frac{dy}{dt} = \mu/x$$

here is how we solve this set of equations. Let \(\mu=1\).

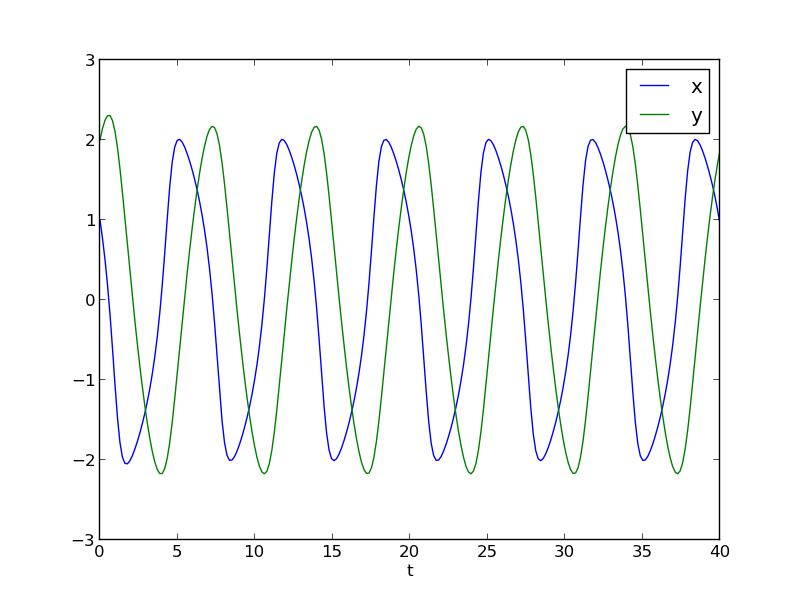
from scipy.integrate import odeint
import numpy as np

mu = 1.0

def vanderpol(X, t):
    x = X[0]
    y = X[1]
    dxdt = mu * (x - 1./3.*x**3 - y)
    dydt = x / mu
    return [dxdt, dydt]

X0 = [1, 2]
t = np.linspace(0, 40, 250)

sol = odeint(vanderpol, X0, t)

import matplotlib.pyplot as plt
x = sol[:, 0]
y = sol[:, 1]

plt.plot(t,x, t, y)
plt.xlabel('t')
plt.legend(('x', 'y'))
plt.savefig('images/vanderpol-1.png')

# phase portrait
plt.figure()
plt.plot(x,y)
plt.plot(x[0], y[0], 'ro')
plt.xlabel('x')
plt.ylabel('y')
plt.savefig('images/vanderpol-2.png')

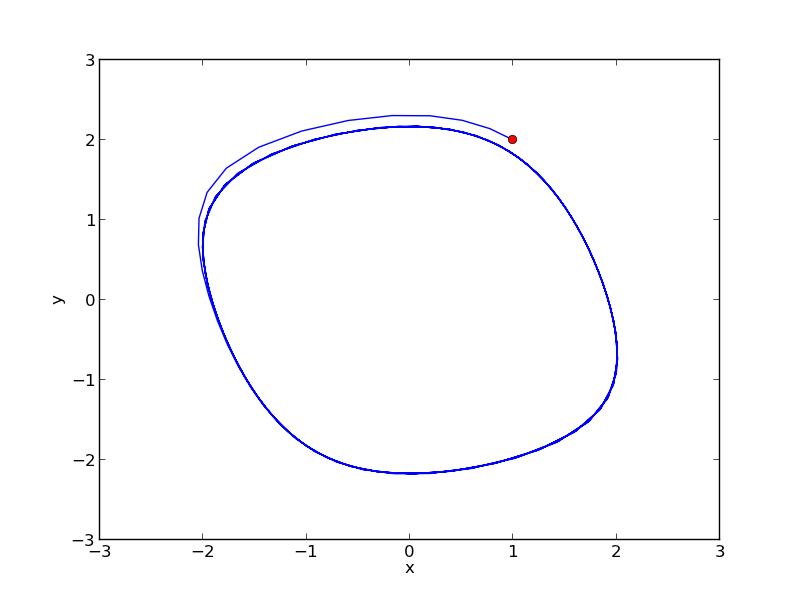
Here is the phase portrait. You can see that a limit cycle is approached, indicating periodicity in the solution.

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source