On the quad or trapz'd in ChemE heaven
Posted February 02, 2013 at 09:00 AM | categories: python, integration | tags:
Updated February 27, 2013 at 02:53 PM
What is the difference between quad and trapz? The short answer is that quad integrates functions (via a function handle) using numerical quadrature, and trapz performs integration of arrays of data using the trapezoid method.
Let us look at some examples. We consider the example of computing \(\int_0^2 x^3 dx\). the analytical integral is \(1/4 x^4\), so we know the integral evaluates to 16/4 = 4. This will be our benchmark for comparison to the numerical methods.
We use the scipy.integrate.quad command to evaluate this \(\int_0^2 x^3 dx\).
from scipy.integrate import quad ans, err = quad(lambda x: x**3, 0, 2) print ans
4.0
you can also define a function for the integrand.
from scipy.integrate import quad def integrand(x): return x**3 ans, err = quad(integrand, 0, 2) print ans
4.0
1 Numerical data integration
if we had numerical data like this, we use trapz to integrate it
import numpy as np x = np.array([0, 0.5, 1, 1.5, 2]) y = x**3 i2 = np.trapz(y, x) error = (i2 - 4)/4 print i2, error
4.25 0.0625
Note the integral of these vectors is greater than 4! You can see why here.
import numpy as np import matplotlib.pyplot as plt x = np.array([0, 0.5, 1, 1.5, 2]) y = x**3 x2 = np.linspace(0, 2) y2 = x2**3 plt.plot(x, y, label='5 points') plt.plot(x2, y2, label='50 points') plt.legend() plt.savefig('images/quad-1.png')
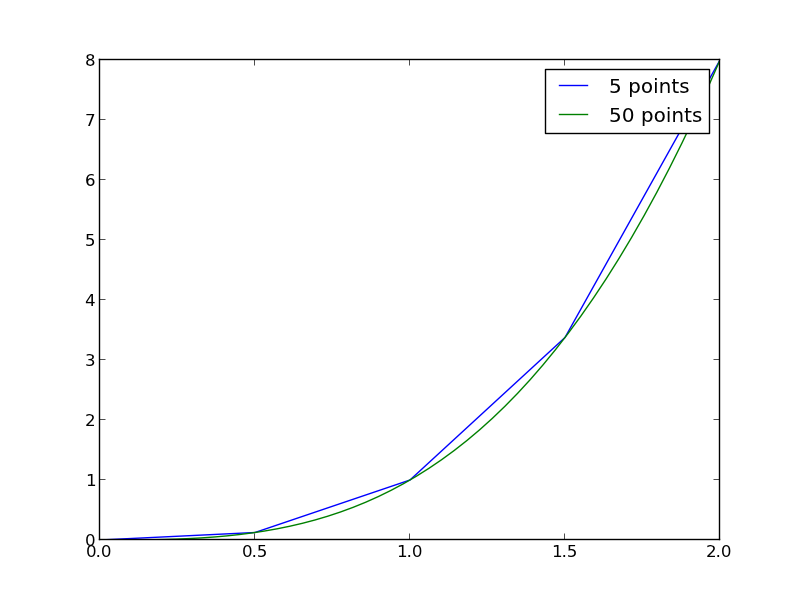
The trapezoid method is overestimating the area significantly. With more points, we get much closer to the analytical value.
import numpy as np x2 = np.linspace(0, 2, 100) y2 = x2**3 print np.trapz(y2, x2)
4.00040812162
2 Combining numerical data with quad
You might want to combine numerical data with the quad function if you want to perform integrals easily. Let us say you are given this data:
x = [0 0.5 1 1.5 2]; y = [0 0.1250 1.0000 3.3750 8.0000];
and you want to integrate this from x = 0.25 to 1.75. We do not have data in those regions, so some interpolation is going to be needed. Here is one approach.
from scipy.interpolate import interp1d from scipy.integrate import quad import numpy as np x = [0, 0.5, 1, 1.5, 2] y = [0, 0.1250, 1.0000, 3.3750, 8.0000] f = interp1d(x, y) # numerical trapezoid method xfine = np.linspace(0.25, 1.75) yfine = f(xfine) print np.trapz(yfine, xfine) # quadrature with interpolation ans, err = quad(f, 0.25, 1.75) print ans
2.53199187838 2.53125
These approaches are very similar, and both rely on linear interpolation. The second approach is simpler, and uses fewer lines of code.
3 Summary
trapz and quad are functions for getting integrals. Both can be used with numerical data if interpolation is used. The syntax for the quad and trapz function is different in scipy than in Matlab.
Finally, see this post for an example of solving an integral equation using quad and fsolve.
Copyright (C) 2013 by John Kitchin. See the License for information about copying.