Find the minimum distance from a point to a curve.
Posted February 14, 2013 at 09:00 AM | categories: optimization | tags:
Updated February 27, 2013 at 02:44 PM
A problem that can be cast as a constrained minimization problem is to find the minimum distance from a point to a curve. Suppose we have \(f(x) = x^2\), and the point (0.5, 2). what is the minimum distance from that point to \(f(x)\)?
import numpy as np import matplotlib.pyplot as plt from scipy.optimize import fmin_cobyla P = (0.5, 2) def f(x): return x**2 def objective(X): x,y = X return np.sqrt((x - P[0])**2 + (y - P[1])**2) def c1(X): x,y = X return f(x) - y X = fmin_cobyla(objective, x0=[0.5,0.5], cons=[c1]) print 'The minimum distance is {0:1.2f}'.format(objective(X)) # Verify the vector to this point is normal to the tangent of the curve # position vector from curve to point v1 = np.array(P) - np.array(X) # position vector v2 = np.array([1, 2.0 * X[0]]) print 'dot(v1, v2) = ',np.dot(v1, v2) x = np.linspace(-2, 2, 100) plt.plot(x, f(x), 'r-', label='f(x)') plt.plot(P[0], P[1], 'bo', label='point') plt.plot([P[0], X[0]], [P[1], X[1]], 'b-', label='shortest distance') plt.plot([X[0], X[0] + 1], [X[1], X[1] + 2.0 * X[0]], 'g-', label='tangent') plt.axis('equal') plt.xlabel('x') plt.ylabel('y') plt.legend(loc='best') plt.savefig('images/min-dist-p-func.png')
The minimum distance is 0.86 dot(v1, v2) = 0.000336477214214 Normal return from subroutine COBYLA NFVALS = 44 F = 8.579598E-01 MAXCV = 0.000000E+00 X = 1.300793E+00 1.692061E+00
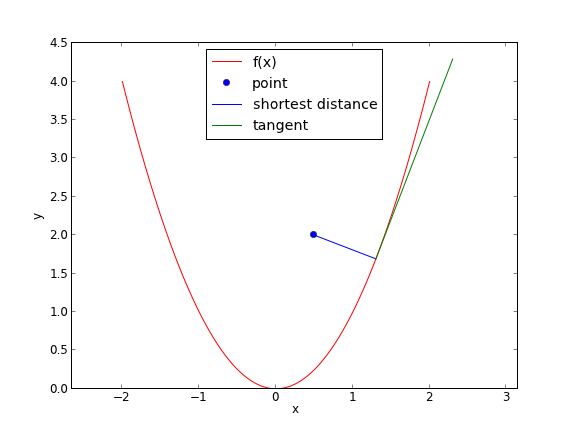
In the code above, we demonstrate that the point we find on the curve that minimizes the distance satisfies the property that a vector from that point to our other point is normal to the tangent of the curve at that point. This is shown by the fact that the dot product of the two vectors is very close to zero. It is not zero because of the accuracy criteria that is used to stop the minimization is not high enough.
Copyright (C) 2013 by John Kitchin. See the License for information about copying.