Solving parameterized ODEs over and over conveniently
Posted February 07, 2013 at 09:00 AM | categories: ode | tags: reaction engineering
Updated March 06, 2013 at 04:38 PM
Matlab post Sometimes we have an ODE that depends on a parameter, and we want to solve the ODE for several parameter values. It is inconvenient to write an ode function for each parameter case. Here we examine a convenient way to solve this problem; we pass the parameter to the ODE at runtime. We consider the following ODE:
$$\frac{dCa}{dt} = -k Ca(t)$$
where \(k\) is a parameter, and we want to solve the equation for a couple of values of \(k\) to test the sensitivity of the solution on the parameter. Our question is, given \(Ca(t=0)=2\), how long does it take to get \(Ca = 1\), and how sensitive is the answer to small variations in \(k\)?
import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt def myode(Ca, t, k): 'ODE definition' dCadt = -k * Ca return dCadt tspan = np.linspace(0, 0.5) k0 = 2 Ca0 = 2 plt.figure(); plt.clf() for k in [0.95 * k0, k0, 1.05 * k0]: sol = odeint(myode, Ca0, tspan, args=(k,)) plt.plot(tspan, sol, label='k={0:1.2f}'.format(k)) print 'At t=0.5 Ca = {0:1.2f} mol/L'.format(sol[-1][0]) plt.legend(loc='best') plt.xlabel('Time') plt.ylabel('$C_A$ (mol/L)') plt.savefig('images/parameterized-ode1.png')
At t=0.5 Ca = 0.77 mol/L At t=0.5 Ca = 0.74 mol/L At t=0.5 Ca = 0.70 mol/L
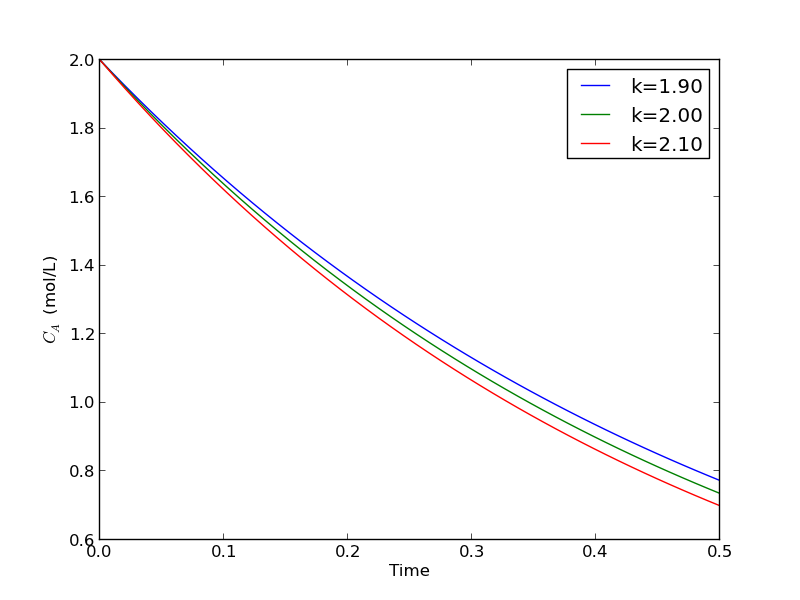
You can see there are some variations in the concentration at t = 0.5. You could over or underestimate the concentration if you have the wrong estimate of $k$! You have to use some judgement here to decide how long to run the reaction to ensure a target goal is met.
Copyright (C) 2013 by John Kitchin. See the License for information about copying.