The Kitchin Research Group

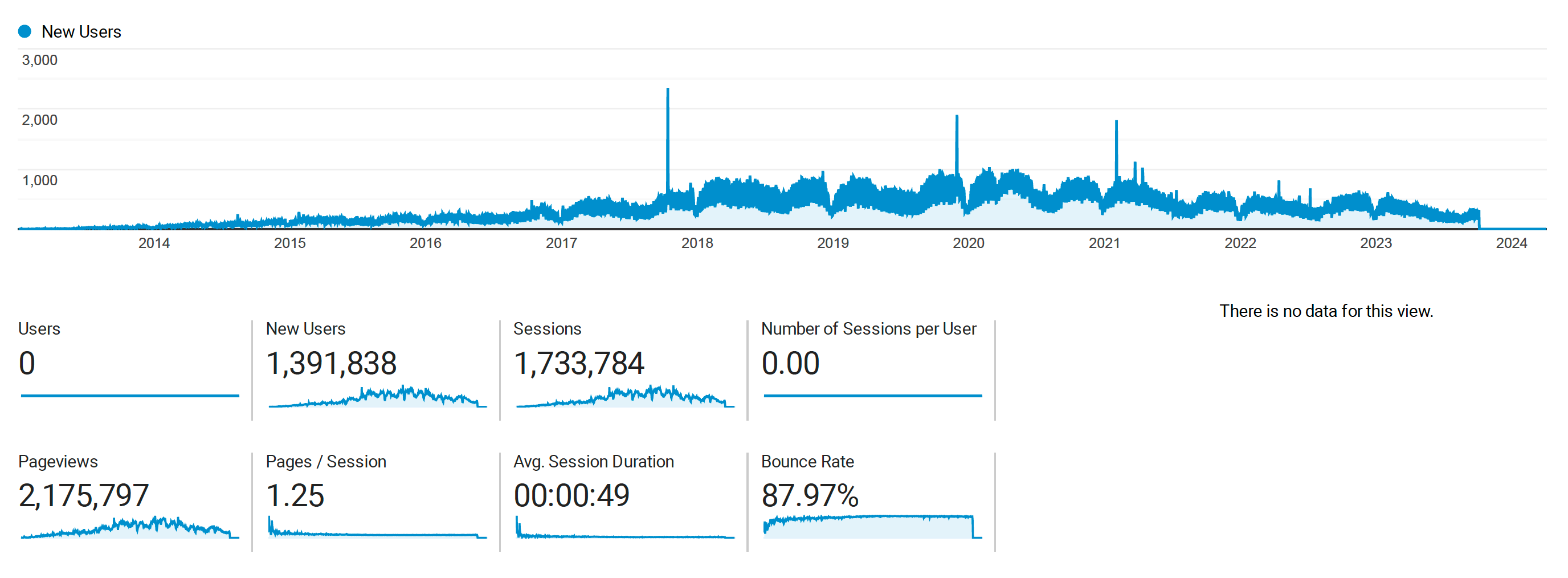
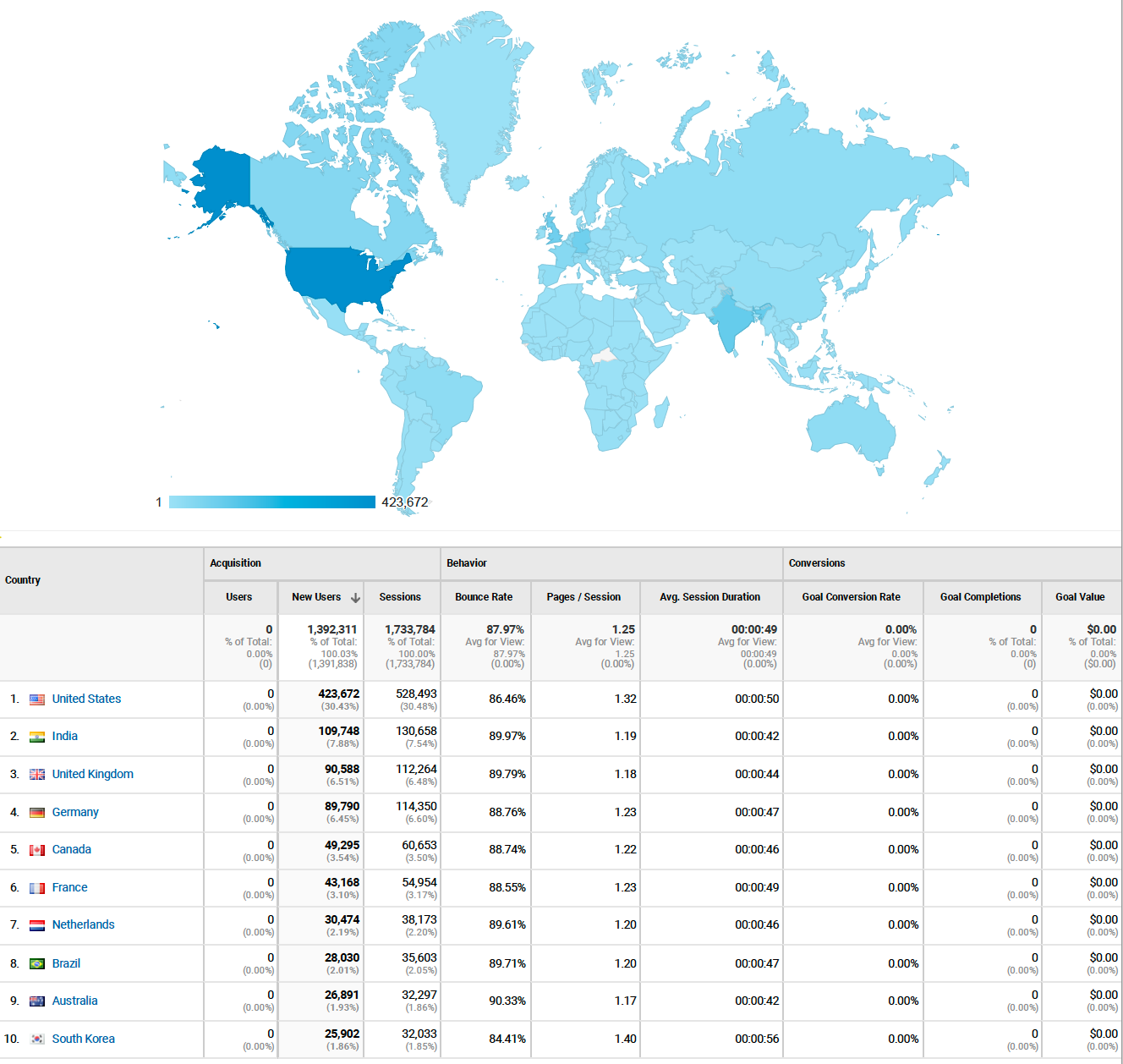
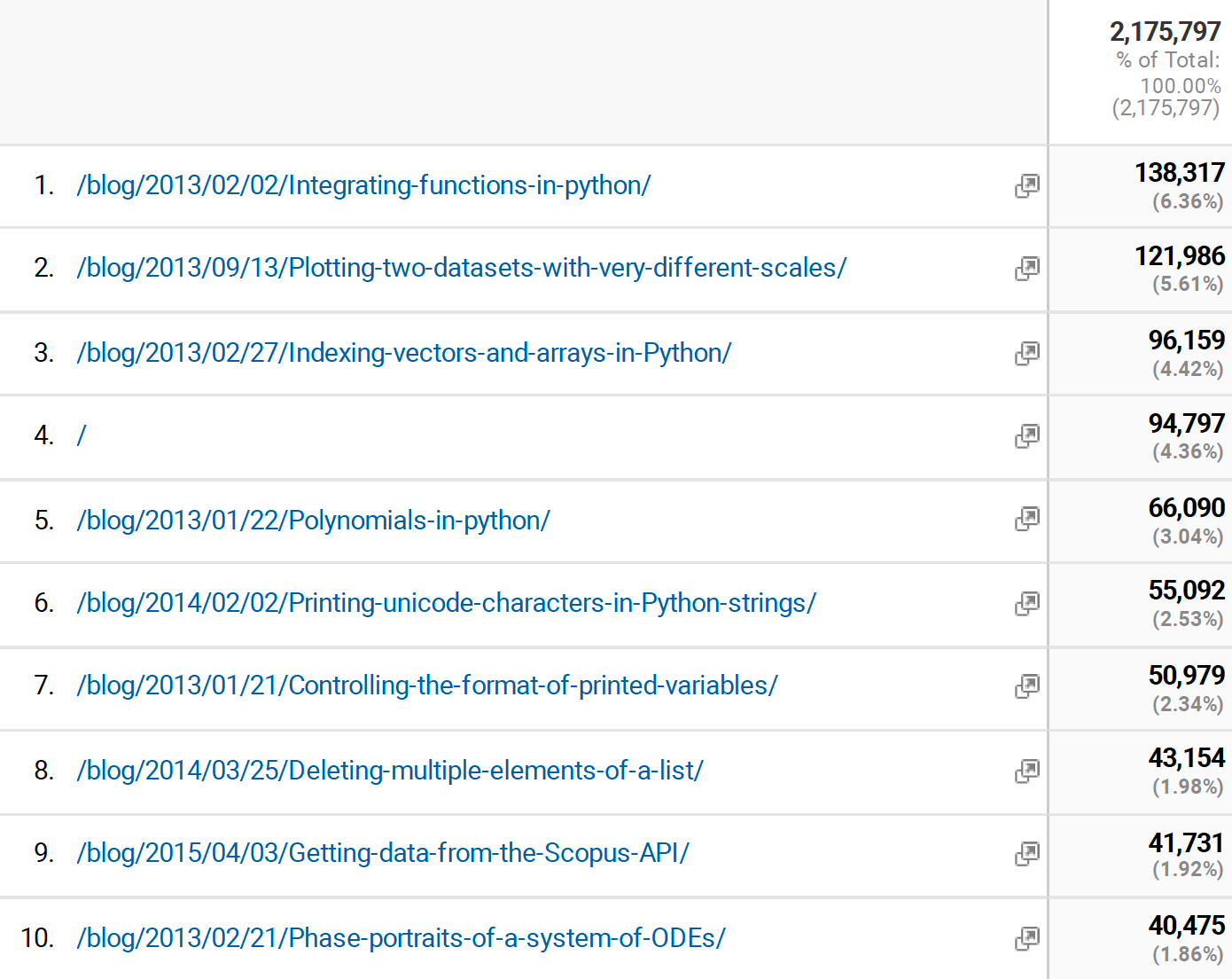
Geometry optimization is an expensive part of DFT; each step requires a DFT step. The Open Catalyst Project provides pre-trained machine learned potentials that provide cheap forces for a broad range of metallic, intermetallic materials. In this work we use models trained on the OC20 dataset to accelerate geometry optimization of materials outside that domain including larger adsorbates, oxides, and zeolites. With fine-tuning, we are able to reduce the number of DFT calls required substantially for these systems.

@article{10.1088/2632-2153/ad37f0,
        author={Wang, Xiaoxiao and Musielewicz, Joseph and Tran, Richard and Ethirajan, Sudheesh Kumar and Fu, Xiaoyan and Mera, Hilda and Kitchin, John R and Kurchin, Rachel and Ulissi, Zachary W},
        title={Generalization of Graph-Based Active Learning Relaxation Strategies Across Materials},
        journal={Machine Learning: Science and Technology},
        url={http://iopscience.iop.org/article/10.1088/2632-2153/ad37f0},
        year={2024}
}

Copyright (C) 2024 by John Kitchin. See the License for information about copying.

org-mode source

Org-mode version = 9.7-pre

There are a few early entries I backdated, but this blog got started in its present form in January 2013. This entry marks entry #594. I started this blog as part of an exercise in switching from Matlab to Python, and the first hundred entries or so are just me solving a problem in Python that I had previously solved in Matlab. It then expanded to include lots of entries on Emacs and org-mode, and other research related topics from my group. Many entries simply document something I spent time working out and that I wanted to be able to find by Google later.

When I set the blog up, I enabled Google Analytics to see if anyone would look at. Recently Google announced they are shutting down the version of analytics I was using, and transitioning to a newer approach. They no longer collect data with the version this blog is using (since Oct last year), and they will delete the data this summer, so today I downloaded some of it to see what has happened over the past decade.

Anecdotally many people from around the world have told me how useful the blog was for them. Now, I have data to see how many people have been impacted by this blog. This figure shows that a lot of people spent time in some part of the blog over the past decade! The data suggests over 1M people viewed these pages over 2M times.

The peak usage was around 2020, and it has been trailing off since then. I have not been as active in posting since then. You can also see there is a very long build up to that peak.

The user group for the blog is truly world wide, including almost every country in this map. That is amazing!

Finally, I found the pages that were most viewed. It is interesting most of them are the older pages, and all about Python. I guess that means I should write more posts on Python.

I don't know what the future of the blog is. It is in need of an overhaul. The packages that build it still work, but are not actively maintained. I have also spent more time writing with Jupyter Book lately than the way I wrote this blog. It isn't likely to disappear any time soon, it sits rent-free in GitHUB pages.

To conclude, to everyone who has read these pages, thank you! It has been a lot of work to put together over the years, and I am glad to see many people have taken a look at it.

Copyright (C) 2024 by John Kitchin. See the License for information about copying.

org-mode source

Org-mode version = 9.7-pre

Modeling magnetic materials with DFT is hard. In this work we develop a machine learning approach to predicting magnetic properties of materials based on their structure. Our two stage model first predicts if a material is magnetic, and then if it is, what the magnetic moments on each atom are. We show this can lead to faster and lower energy DFT solutions.

@article{sanspeur-2024-circum-data,
  author =       {Rohan Yuri Sanspeur and John R Kitchin},
  title =        {Circumventing Data Imbalance in Magnetic Ground State Data for
                  Magnetic Moment Predictions},
  journal =      {Machine Learning: Science and Technology},
  volume =       {5},
  number =       {1},
  pages =        {015023},
  year =         2024,
  doi =          {10.1088/2632-2153/ad23fb},
  url =          {http://dx.doi.org/10.1088/2632-2153/ad23fb},
  DATE_ADDED =   {Tue Feb 6 20:13:47 2024},
}

Copyright (C) 2024 by John Kitchin. See the License for information about copying.

org-mode source

Org-mode version = 9.7-pre

In this work, we show that we can use large graph neural networks to predict transition metal complex energies. We developed an improved dataset at a higher level of theory, and tested models ranging from GemNet-T (best) to SchNet (worst). The model performance saturates with the size of neutral structures, and improves with increasing size of charged structures. Finally, we showed that a pre-trained model from OC20 was even better than training from scratch. This indicates a degree of transferability from heterogeneous catalyst models to homogeneous molecular catalysts.

@article{garrison-2023-apply-large,
  author =       {Garrison, Aaron G. and Heras-Domingo, Javier and Kitchin, John
                  R. and dos Passos Gomes, Gabriel and Ulissi, Zachary W. and
                  Blau, Samuel M.},
  title =        {Applying Large Graph Neural Networks To Predict Transition
                  Metal Complex Energies Using the tmQM\_wB97MV Data Set},
  journal =      {Journal of Chemical Information and Modeling},
  volume =       0,
  number =       0,
  pages =        {null},
  year =         2023,
  doi =          {10.1021/acs.jcim.3c01226},
  URL =          {https://doi.org/10.1021/acs.jcim.3c01226},
  eprint =       {https://doi.org/10.1021/acs.jcim.3c01226},
  note =         {PMID: 38049389},
}

Copyright (C) 2023 by John Kitchin. See the License for information about copying.

org-mode source

Org-mode version = 9.7-pre

The electron density is one of the most important quantities we use DFT to calculate. It is the foundation of how we compute energy, forces, and many other properties. DFT is expensive though, so in this work we show that we can build a graph neural network that can be used to predict electron densities directly from the atomic coordinates of a system. We show that the predicted densities can also be used to estimate dipole moments and Bader charges.

@article{sunshine-2023-chemic-proper,
  author =       {Sunshine, Ethan M. and Shuaibi, Muhammed and Ulissi, Zachary
                  W. and Kitchin, John R.},
  title =        {Chemical Properties From Graph Neural Network-Predicted
                  Electron Densities},
  journal =      {The Journal of Physical Chemistry C},
  volume =       0,
  number =       0,
  pages =        {null},
  year =         2023,
  doi =          {10.1021/acs.jpcc.3c06157},
  url =          {https://doi.org/10.1021/acs.jpcc.3c06157},
  eprint =       {https://doi.org/10.1021/acs.jpcc.3c06157},
}

Copyright (C) 2023 by John Kitchin. See the License for information about copying.

org-mode source

Org-mode version = 9.7-pre