The Kitchin Research Group

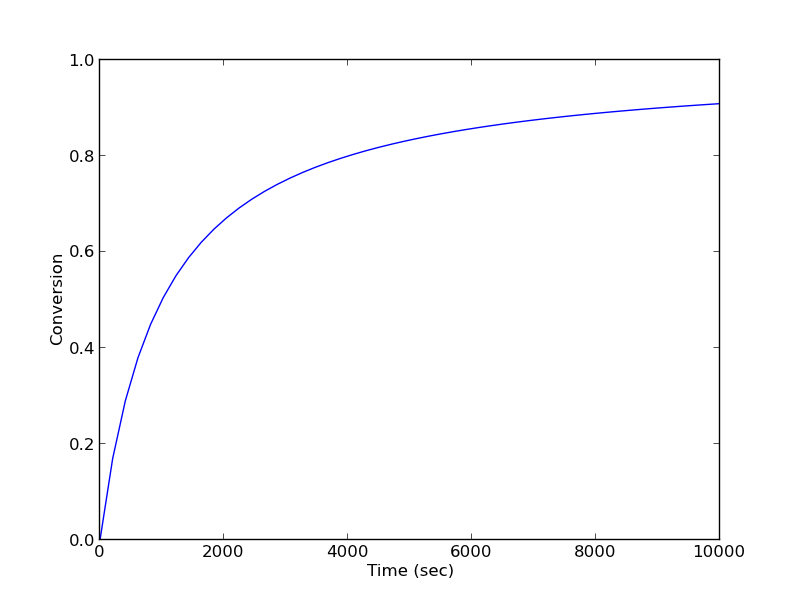
For a constant volume batch reactor where \(A \rightarrow B\) at a rate of \(-r_A = k C_A^2\), we derive the following design equation for the length of time required to achieve a particular level of conversion :

\(t(X) = \frac{1}{k C_{A0}} \int_{X=0}^X \frac{dX}{(1-X)^2}\)

if \(k = 10^{-3}\) L/mol/s and \(C_{A0}\) = 1 mol/L, estimate the time to achieve 90% conversion.

We could analytically solve the integral and evaluate it, but instead we will numerically evaluate it using scipy.integrate.quad. This function returns two values: the evaluated integral, and an estimate of the absolute error in the answer.

from scipy.integrate import quad

def integrand(X):
    k = 1.0e-3
    Ca0 = 1.0  # mol/L
    return 1./(k*Ca0)*(1./(1-X)**2)

sol, abserr = quad(integrand, 0, 0.9)
print 't = {0} seconds ({1} hours)'.format(sol, sol/3600)
print 'Estimated absolute error = {0}'.format(abserr)

t = 9000.0 seconds (2.5 hours)
Estimated absolute error = 2.12203274482e-07

You can see the estimate error is very small compared to the solution.

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source

An alternative approach of evaluating an integral is to integrate a differential equation. For the batch reactor, the differential equation that describes conversion as a function of time is:

\(\frac{dX}{dt} = -r_A V/N_{A0}\).

Given a value of initial concentration, or volume and initial number of moles of A, we can integrate this ODE to find the conversion at some later time. We assume that \(X(t=0)=0\). We will integrate the ODE over a time span of 0 to 10,000 seconds.

from scipy.integrate import odeint
import numpy as np
import matplotlib.pyplot as plt

k = 1.0e-3
Ca0 = 1.0  # mol/L

def func(X, t):
    ra = -k * (Ca0 * (1 - X))**2
    return -ra / Ca0

X0 = 0
tspan = np.linspace(0,10000)

sol = odeint(func, X0, tspan)
plt.plot(tspan,sol)
plt.xlabel('Time (sec)')
plt.ylabel('Conversion')
plt.savefig('images/2013-01-06-batch-conversion.png')

You can read off of this figure to find the time required to achieve a particular conversion.

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source

Congratulations Zhongnan!

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source

Bin Liu has joined us as a postdoc from Argonne National Lab. He will be working on superalloy oxidation.

Steve Illes has joined us as a PhD student from Purdue University. He will be using Raman spectroscopy to investigate electrode surfaces under oxygen evolution conditions.

Jacob Boes has also joined us as a PhD student. He will be using DFT to study multicomponent alloys.

Prateek Mehta has joined the group as an MS student. He will be working on predicting oxide polymorph stability.

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source

Matt will be visiting the University of Seoul, Korea to collaborate with Jeong Woo Han in the summer of 2013! This fellowship is supported by the IMI Program of the National Science Foundation under Award No. DMR 08-43934 through UC Santa Barbara. Congratulations Matt!

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source