The Kitchin Research Group

It is common to evaluate a function for a range of values. Let us consider the value of the function \(f(x) = \cos(x)\) over the range of \(0 < x < \pi\). We cannot consider every value in that range, but we can consider say 10 points in the range. The nil conveniently creates an array of values.

import numpy as np
print np.linspace(0, np.pi, 10)

[ 0.          0.34906585  0.6981317   1.04719755  1.3962634   1.74532925
  2.0943951   2.44346095  2.7925268   3.14159265]

The main point of using the nil functions is that they work element-wise on elements of an array. In this example, we compute the \(\cos(x)\) for each element of \(x\).

import numpy as np
x = np.linspace(0, np.pi, 10)
print np.cos(x)

[ 1.          0.93969262  0.76604444  0.5         0.17364818 -0.17364818
 -0.5        -0.76604444 -0.93969262 -1.        ]

You can already see from this output that there is a root to the equation \(\cos(x) = 0\), because there is a change in sign in the output. This is not a very convenient way to view the results; a graph would be better. We use nil to make figures. Here is an example.

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, np.pi, 10)
plt.plot(x, np.cos(x))
plt.xlabel('x')
plt.ylabel('cos(x)')
plt.savefig('images/plot-cos.png')

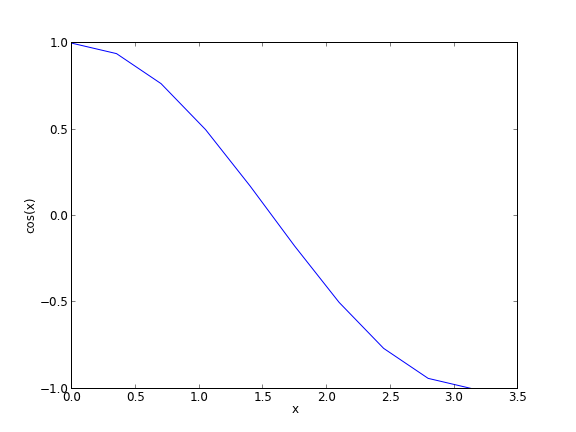
This figure illustrates graphically what the numbers above show. The function crosses zero at approximately \(x = 1.5\). To get a more precise value, we must actually solve the function numerically. We use the function nil to do that. More precisely, we want to solve the equation \(f(x) = \cos(x) = 0\). We create a function that defines that equation, and then use nil to solve it.

from scipy.optimize import fsolve 
import numpy as np

def f(x):
    return np.cos(x)

sol, = fsolve(f, x0=1.5) # the comma after sol makes it return a float
print sol
print np.pi / 2

1.57079632679
1.57079632679

We know the solution is π/2.

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source

Compare what's here to the Matlab implementation.

We often need to make functions in our codes to do things.

def f(x):
    "return the inverse square of x"
    return 1.0 / x**2

print f(3)
print f([4,5])

... ... >>> 0.111111111111
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "<stdin>", line 3, in f
TypeError: unsupported operand type(s) for ** or pow(): 'list' and 'int'

Note that functions are not automatically vectorized. That is why we see the error above. There are a few ways to achieve that. One is to “cast” the input variables to objects that support vectorized operations, such as numpy.array objects.

import numpy as np

def f(x):
    "return the inverse square of x"
    x = np.array(x)
    return 1.0 / x**2

print f(3)
print f([4,5])

>>> ... ... ... ... >>> 0.111111111111
[ 0.0625  0.04  ]

It is possible to have more than one variable.

import numpy as np

def func(x, y):
    "return product of x and y"
    return x * y

print func(2, 3)
print func(np.array([2, 3]), np.array([3, 4]))

6
[ 6 12]

You can define “lambda” functions, which are also known as inline or anonymous functions. The syntax is lambda var:f(var). I think these are hard to read and discourage their use. Here is a typical usage where you have to define a simple function that is passed to another function, e.g. scipy.integrate.quad to perform an integral.

from scipy.integrate import quad
print quad(lambda x:x**3, 0 ,2)

(4.0, 4.440892098500626e-14)

It is possible to nest functions inside of functions like this.

def wrapper(x):
    a = 4
    def func(x, a):
        return a * x

    return func(x, a)

print wrapper(4)

16

An alternative approach is to “wrap” a function, say to fix a parameter. You might do this so you can integrate the wrapped function, which depends on only a single variable, whereas the original function depends on two variables.

def func(x, a):
        return a * x
 
def wrapper(x):
    a = 4
    return func(x, a)

print wrapper(4)

16

Last example, defining a function for an ode

from scipy.integrate import odeint
import numpy as np
import matplotlib.pyplot as plt

k = 2.2
def myode(t,y):
    "ode defining exponential growth"
    return k * t

y0 = 3
tspan = np.linspace(0,1)
y =  odeint(myode, y0, tspan)

plt.plot(tspan, y)
plt.xlabel('Time')
plt.ylabel('y')
plt.savefig('images/funcs-ode.png')

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source

We can combine operations to evaluate complex equations. Consider the value of the equation \(x^3 - \log(x)\) for the value \(x=4.1\).

import numpy as np
x = 3
print x**3 - np.log(x)

25.9013877113

It would be tedious to type this out each time. Next, we learn how to express this equation as a new function, which we can call with different values.

import numpy as np
def f(x):
    return x**3 - np.log(x)

print f(3)
print f(5.1)

25.9013877113
131.02175946

It may not seem like we did much there, but this is the foundation for solving equations in the future. Before we get to solving equations, we have a few more details to consider. Next, we consider evaluating functions on arrays of values.

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source

The primary library we will consider is nil, which provides many mathematical functions, statistics as well as support for linear algebra. For a complete listing of the functions available, see http://docs.scipy.org/doc/numpy/reference/routines.math.html. We begin with the simplest functions.

import numpy as np
print np.sqrt(2)

1.41421356237

import numpy as np
print np.exp(1)

2.71828182846

import numpy as np
print np.log(10)
print np.log10(10)  # base10

2.30258509299
1.0

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source

Matlab post

Occasionally it is important to have sorted data. Python has a few sorting options.

a = [4, 5, 1, 6, 8, 3, 2]
print a
a.sort()  # inplace sorting
print a

a.sort(reverse=True)
print a

[4, 5, 1, 6, 8, 3, 2]
[1, 2, 3, 4, 5, 6, 8]
[8, 6, 5, 4, 3, 2, 1]

If you do not want to modify your list, but rather get a copy of a sorted list, use the sorted command.

a = [4, 5, 1, 6, 8, 3, 2]
print 'sorted a = ',sorted(a)  # no change to a
print 'sorted a = ',sorted(a, reverse=True)  # no change to a
print 'a        = ',a

sorted a =  [1, 2, 3, 4, 5, 6, 8]
sorted a =  [8, 6, 5, 4, 3, 2, 1]
a        =  [4, 5, 1, 6, 8, 3, 2]

This works for strings too:

a = ['b', 'a', 'c', 'tree']
print sorted(a)

['a', 'b', 'c', 'tree']

Here is a subtle point though. A capitalized letter comes before a lowercase letter. We can pass a function to the sorted command that is called on each element prior to the sort. Here we make each word lower case before sorting.

a = ['B', 'a', 'c', 'tree']
print sorted(a)

# sort by lower case letter
print sorted(a, key=str.lower)

['B', 'a', 'c', 'tree']
['a', 'B', 'c', 'tree']

Here is a more complex sorting problem. We have a list of tuples with group names and the letter grade. We want to sort the list by the letter grades. We do this by creating a function that maps the letter grades to the position of the letter grades in a sorted list. We use the list.index function to find the index of the letter grade, and then sort on that.

groups = [('group1', 'B'),
          ('group2', 'A+'),
          ('group3', 'A')]

def grade_key(gtup):
    '''gtup is a tuple of ('groupname', 'lettergrade')'''
    lettergrade = gtup[1]

    grades = ['A++', 'A+', 'A', 'A-', 'A/B'
              'B+', 'B', 'B-', 'B/C',
              'C+', 'C', 'C-', 'C/D',
              'D+', 'D', 'D-', 'D/R',
              'R+', 'R', 'R-', 'R--']
    
    return grades.index(lettergrade)

print sorted(groups, key=grade_key)

[('group2', 'A+'), ('group3', 'A'), ('group1', 'B')]

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source