Now, let us consider a Fortran code with two files. We will define a module file, and a program file. The module file contains a function to compute the area of a circle as a function of its radius. Here is our module file, which is tangled to circle.f90.
MODULE Circle
implicit None
public :: area
contains
function area(r)
implicit none
real, intent(in) :: r
real :: area
area = 3.14159 * r**2
return
end function area
END MODULE Circle
Now, we write a program that will print a table of circle areas. Here we hard-code an array of 5 radius values, then loop through the values and get the area of the circle with that radius. We will print some output that generates an org-mode table . In this program, we use our module defined above.
program main
use circle, only: area
implicit none
integer :: i
REAL, DIMENSION(5) :: R
R = (/1.0, 2.0, 3.0, 4.0, 5.0 /)
print *, "#+tblname: circle-area"
do i = 1, 5
print *, "|", R(i), "|", area(R(i)), "|"
end do
end program main
Now, we make a makefile that will build this program. I use a different name for the file, since we already have a Makefile in this directory from the last example. I also put @ at the front of each command in the makefile to suppress it from being echoed when we run it. Later, we will use the makefile to compile the program, and then run it, and we only want the output of the program.
The compiling instructions are more complex. We have to compile the circle module first, and then the main program. Here is our makefile.
circle:
@gfortran -c circle.f90
main: circle
@gfortran -c main.f90
@gfortran circle.o main.o -o main
clean:
@rm -f *.o main
Now, we run this block, which tangles out our new files.
| main.f90 |
circle.f90 |
hello.f90 |
makefile-main |
Makefile |
Note that results above show we have tangled all the source blocks in this file. You can limit the scope of tangling, by narrowing to a subtree, but that is beyond our aim for today.
Finally, we are ready to build our program. We specify the new makefile with the -f option to make. We use the clean target to get rid of old results, and then the main target with builds the program. Since main depends on circle, the circle file is compiled first.
Note in this block I use this header:
#+BEGIN_SRC sh :results raw
That will tell the block to output the results directly in the buffer. I have the fortran code prename the table, and put | around the entries, so this entry is output directly as an org table.
make -f makefile-main clean main
./main
| 1.000000 |
3.141590 |
| 2.000000 |
12.56636 |
| 3.000000 |
28.27431 |
| 4.000000 |
50.26544 |
| 5.000000 |
78.53975 |
It takes some skill getting used to using :results raw. The results are not replaced if you run the code again. That can be inconvenient if you print a very large table, which you must manually delete.
Now that we have a named org table, I can use that table as data in other source blocks, e.g. here in python. You define variables in the header name by referring to the tblname like this.
#+BEGIN_SRC python :var data=circle-area
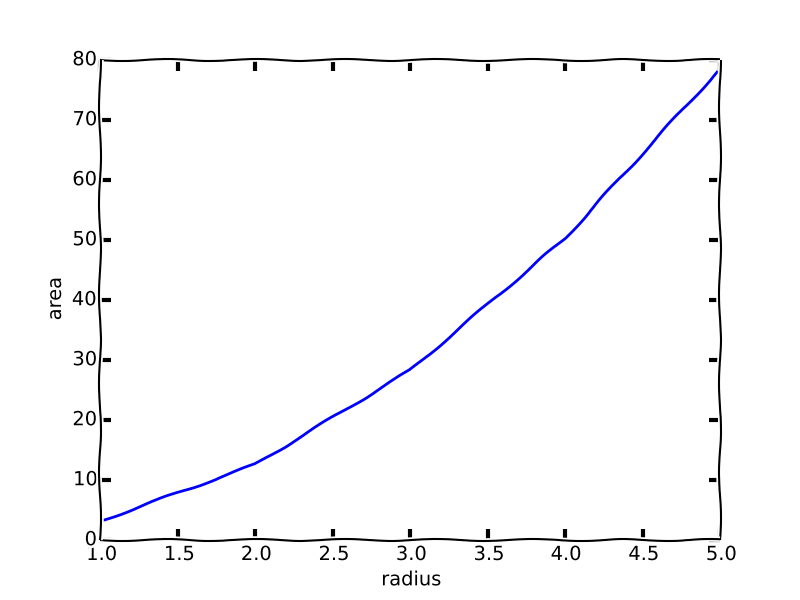
Then, data is available as a variable in your code. Let us try it and plot the area vs. radius here. For more fun, we will make the plot xkcd , so it looks like I sketched it by hand.
import numpy as np
import matplotlib.pyplot as plt
plt.xkcd()
print data # data is a list
data = np.array(data)
plt.plot(data[:, 0], data[:, 1])
plt.xlabel('radius')
plt.ylabel('area')
plt.savefig('circle-area.png')
[[1.0, 3.14159], [2.0, 12.56636], [3.0, 28.27431], [4.0, 50.26544], [5.0, 78.53975]]
It appears the area increases quadratically with radius. No surprise there! For fun, let us show that. If we divide each area by \(r^2\), we should get back π. Let us do this in emacs-lisp, just to illustrate how flexibly we can switch between languages. In lisp, the data structure will be a list of items like ((radius1 area1) (radius2 area2)…). So, we just map a function that divides the area (the second element of an entry) by the square of the first element. My lisp-fu is only average, so I use the nth function to get those elements. We also load the calc library to get the math-pow function.
(require 'calc)
(mapcar (lambda (x) (/ (nth 1 x) (math-pow (nth 0 x) 2))) data)
| 3.14159 |
3.14159 |
3.14159 |
3.14159 |
3.14159 |
Indeed, we get π for each element, which shows in fact that the area does increase quadratically with radius.
You can learn more about tangling source code from org-mode here http://orgmode.org/manual/Extracting-source-code.html .