Today we examine an approach to fitting curves to overlapping peaks to deconvolute them so we can estimate the area under each curve. We have a text file that contains data from a gas chromatograph with two peaks that overlap. We want the area under each peak to estimate the gas composition. You will see how to read the text file in, parse it to get the data for plotting and analysis, and then how to fit it.
A line like “# of Points 9969” tells us the number of points we have to read. The data starts after a line containing “R.Time Intensity”. Here we read the number of points, and then get the data into arrays.
import numpy as np
import matplotlib.pyplot as plt
datafile = 'data/gc-data-21.txt'
i = 0
with open(datafile) as f:
lines = f.readlines()
for i,line in enumerate(lines):
if '# of Points' in line:
npoints = int(line.split()[-1])
elif 'R.Time Intensity' in line:
i += 1
break
# now get the data
t, intensity = [], []
for j in range(i, i + npoints):
fields = lines[j].split()
t += [float(fields[0])]
intensity += [int(fields[1])]
t = np.array(t)
intensity = np.array(intensity)
# now plot the data in the relevant time frame
plt.plot(t, intensity)
plt.xlim([4, 6])
plt.xlabel('Time (s)')
plt.ylabel('Intensity (arb. units)')
plt.savefig('images/deconvolute-1.png')
>>> >>> >>> >>> >>> ... ... >>> ... ... ... ... ... ... >>> ... >>> ... ... ... ... >>> >>> >>> >>> ... [<matplotlib.lines.Line2D object at 0x04CE6CF0>]
(4, 6)
<matplotlib.text.Text object at 0x04BBB950>
<matplotlib.text.Text object at 0x04BD0A10>
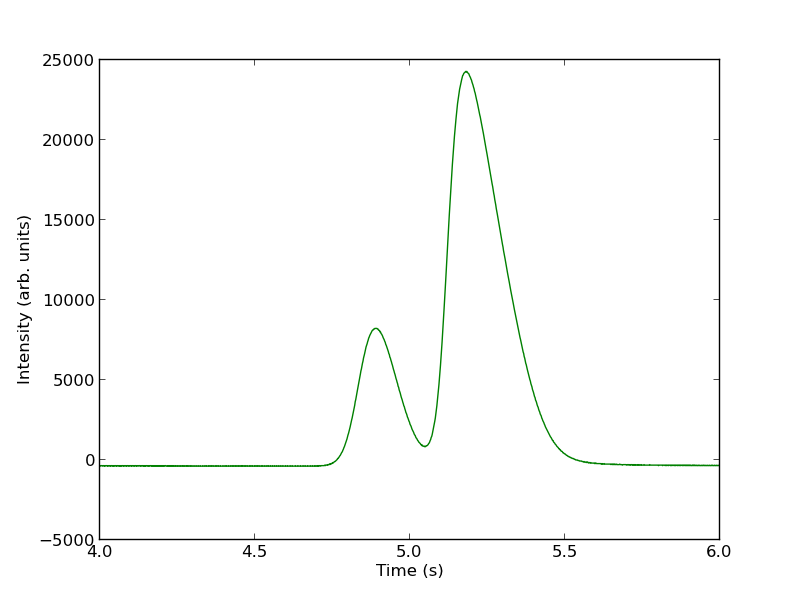
You can see there is a non-zero baseline. We will normalize that by the average between 4 and 4.4 seconds.
intensity -= np.mean(intensity[(t> 4) & (t < 4.4)])
plt.figure()
plt.plot(t, intensity)
plt.xlim([4, 6])
plt.xlabel('Time (s)')
plt.ylabel('Intensity (arb. units)')
plt.savefig('./images/deconvolute-2.png')
<matplotlib.figure.Figure object at 0x04CF7950>
[<matplotlib.lines.Line2D object at 0x04DF5C30>]
(4, 6)
<matplotlib.text.Text object at 0x04DDB690>
<matplotlib.text.Text object at 0x04DE3630>
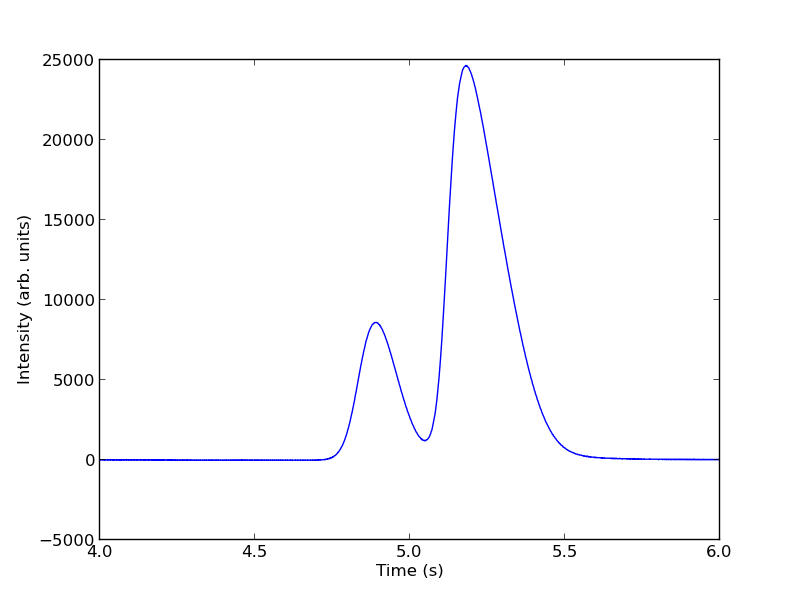
The peaks are asymmetric, decaying gaussian functions. We define a function for this
from scipy.special import erf
def asym_peak(t, pars):
'from Anal. Chem. 1994, 66, 1294-1301'
a0 = pars[0] # peak area
a1 = pars[1] # elution time
a2 = pars[2] # width of gaussian
a3 = pars[3] # exponential damping term
f = (a0/2/a3*np.exp(a2**2/2.0/a3**2 + (a1 - t)/a3)
*(erf((t-a1)/(np.sqrt(2.0)*a2) - a2/np.sqrt(2.0)/a3) + 1.0))
return f
To get two peaks, we simply add two peaks together.
def two_peaks(t, *pars):
'function of two overlapping peaks'
a10 = pars[0] # peak area
a11 = pars[1] # elution time
a12 = pars[2] # width of gaussian
a13 = pars[3] # exponential damping term
a20 = pars[4] # peak area
a21 = pars[5] # elution time
a22 = pars[6] # width of gaussian
a23 = pars[7] # exponential damping term
p1 = asym_peak(t, [a10, a11, a12, a13])
p2 = asym_peak(t, [a20, a21, a22, a23])
return p1 + p2
To show the function is close to reasonable, we plot the fitting function with an initial guess for each parameter. The fit is not good, but we have only guessed the parameters for now.
parguess = (1500, 4.85, 0.05, 0.05, 5000, 5.1, 0.05, 0.1)
plt.figure()
plt.plot(t, intensity)
plt.plot(t,two_peaks(t, *parguess),'g-')
plt.xlim([4, 6])
plt.xlabel('Time (s)')
plt.ylabel('Intensity (arb. units)')
plt.savefig('images/deconvolution-3.png')
<matplotlib.figure.Figure object at 0x04FEF690>
[<matplotlib.lines.Line2D object at 0x05049870>]
[<matplotlib.lines.Line2D object at 0x04FEFA90>]
(4, 6)
<matplotlib.text.Text object at 0x0502E210>
<matplotlib.text.Text object at 0x050362B0>
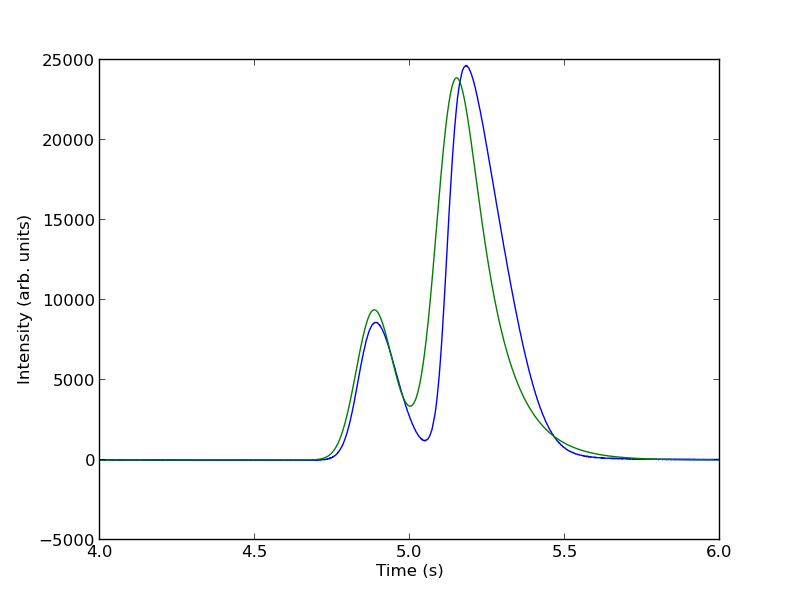
Next, we use nonlinear curve fitting from scipy.optimize.curve_fit
from scipy.optimize import curve_fit
popt, pcov = curve_fit(two_peaks, t, intensity, parguess)
print popt
plt.plot(t, two_peaks(t, *popt), 'r-')
plt.legend(['data', 'initial guess','final fit'])
plt.savefig('images/deconvolution-4.png')
>>> >>> [ 1.31039283e+03 4.87474330e+00 5.55414785e-02 2.50610175e-02
5.32556821e+03 5.14121507e+00 4.68236129e-02 1.04105615e-01]
>>> [<matplotlib.lines.Line2D object at 0x0505BA10>]
<matplotlib.legend.Legend object at 0x05286270>
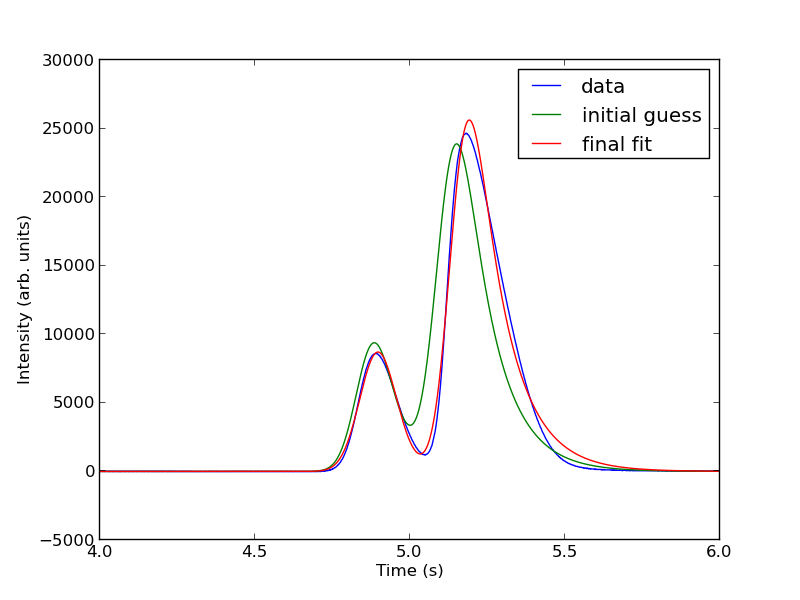
The fits are not perfect. The small peak is pretty good, but there is an unphysical tail on the larger peak, and a small mismatch at the peak. There is not much to do about that, it means the model peak we are using is not a good model for the peak. We will still integrate the areas though.
pars1 = popt[0:4]
pars2 = popt[4:8]
peak1 = asym_peak(t, pars1)
peak2 = asym_peak(t, pars2)
area1 = np.trapz(peak1, t)
area2 = np.trapz(peak2, t)
print 'Area 1 = {0:1.2f}'.format(area1)
print 'Area 2 = {0:1.2f}'.format(area2)
print 'Area 1 is {0:1.2%} of the whole area'.format(area1/(area1 + area2))
print 'Area 2 is {0:1.2%} of the whole area'.format(area2/(area1 + area2))
plt.figure()
plt.plot(t, intensity)
plt.plot(t, peak1, 'r-')
plt.plot(t, peak2, 'g-')
plt.xlim([4, 6])
plt.xlabel('Time (s)')
plt.ylabel('Intensity (arb. units)')
plt.legend(['data', 'peak 1', 'peak 2'])
plt.savefig('images/deconvolution-5.png')
>>> >>> >>> >>> >>> >>> >>> >>> Area 1 = 1310.39
Area 2 = 5325.57
>>> Area 1 is 19.75% of the whole area
Area 2 is 80.25% of the whole area
>>> <matplotlib.figure.Figure object at 0x05286ED0>
[<matplotlib.lines.Line2D object at 0x053A5AB0>]
[<matplotlib.lines.Line2D object at 0x05291D30>]
[<matplotlib.lines.Line2D object at 0x053B9810>]
(4, 6)
<matplotlib.text.Text object at 0x0529C4B0>
<matplotlib.text.Text object at 0x052A3450>
<matplotlib.legend.Legend object at 0x053B9ED0>
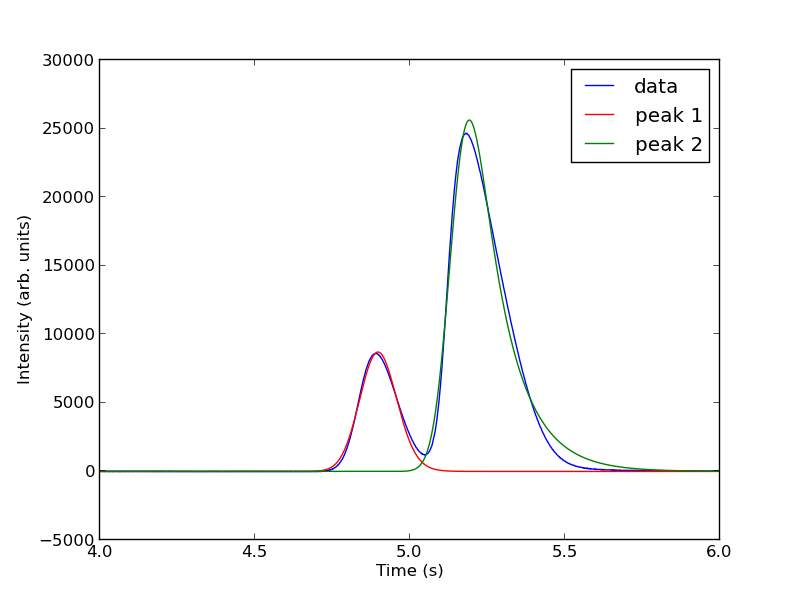
This sample was air, and the first peak is oxygen, and the second peak is nitrogen. we come pretty close to the actual composition of air, although it is low on the oxygen content. To do better, one would have to use a calibration curve.
In the end, the overlap of the peaks is pretty small, but it is still difficult to reliably and reproducibly deconvolute them. By using an algorithm like we have demonstrated here, it is possible at least to make the deconvolution reproducible.
1 Notable differences from Matlab
- The order of arguments to np.trapz is reversed.
- The order of arguments to the fitting function scipy.optimize.curve_fit is different than in Matlab.
- The scipy.optimize.curve_fit function expects a fitting function that has all parameters as arguments, where Matlab expects a vector of parameters.
Copyright (C) 2013 by John Kitchin. See the License for information about copying.
org-mode source