Another look at nonlinear BVPs

Posted March 11, 2013 at 10:44 AM | categories: bvp | tags:

Updated March 11, 2013 at 04:31 PM

Adapted from http://www.mathworks.com/help/matlab/ref/bvp4c.html

Boundary value problems may have more than one solution. Let us consider the BVP:

\begin{eqnarray} y'' + |y| &=& 0 \\ y(0) &=& 0 \\ y(4) &=& -2 \end{eqnarray}

We will see this equation has two answers, depending on your initial guess. We convert this to the following set of coupled equations:

\begin{eqnarray} y_1' &=& y_2 \\ y_2' &=& -|y_1| \\ y_1(0)&=& 0\\ y_1(4) &=& -2 \end{eqnarray}

This BVP is nonlinear because of the absolute value. We will have to guess solutions to get started. We will guess two different solutions, both of which will be constant values. We will use pycse.bvp to solve the equation. 

import numpy as np
from pycse import bvp
import matplotlib.pyplot as plt

def odefun(Y, x):
    y1, y2 = Y
    dy1dx = y2
    dy2dx = -np.abs(y1)
    return [dy1dx, dy2dx]

def bcfun(Ya, Yb):
    y1a, y2a = Ya
    y1b, y2b = Yb

    return [y1a, -2 - y1b]

x = np.linspace(0, 4, 100)

y1 = 1.0 * np.ones(x.shape)
y2 = 0.0 * np.ones(x.shape)

Yinit = np.vstack([y1, y2])

sol = bvp(odefun, bcfun, x, Yinit)

plt.plot(x, sol[0])

# another initial guess
y1 = -1.0 * np.ones(x.shape)
y2 = 0.0 * np.ones(x.shape)

Yinit = np.vstack([y1, y2])

sol = bvp(odefun, bcfun, x, Yinit)

plt.plot(x, sol[0])
plt.legend(['guess 1', 'guess 2'])
plt.savefig('images/bvp-another-nonlin-1.png')
plt.show()

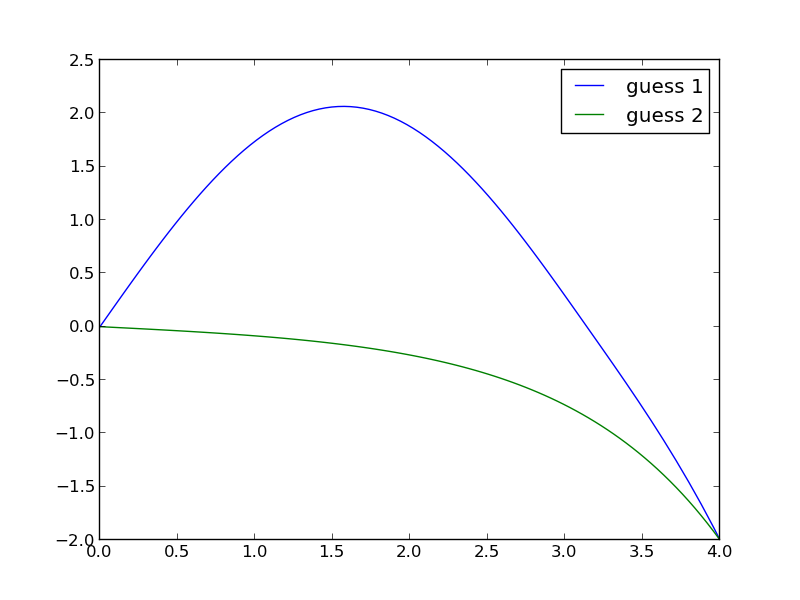
This example shows that a nonlinear BVP may have different solutions, and which one you get depends on the guess you make for the solution. This is analogous to solving nonlinear algebraic equations (which is what is done in solving this problem!).

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source

Discuss on Twitter