Finding minima and maxima in ODE solutions with events

Posted February 27, 2013 at 02:31 PM | categories: ode | tags:

Updated February 27, 2013 at 02:31 PM

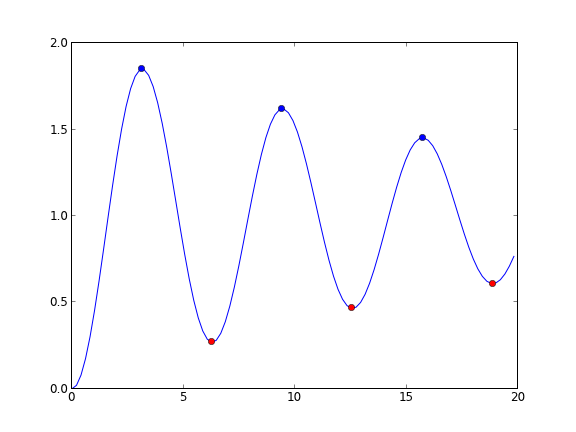
Matlab post Today we look at another way to use events in an ode solver. We use an events function to find minima and maxima, by evaluating the ODE in the event function to find conditions where the first derivative is zero, and approached from the right direction. A maximum is when the fisrt derivative is zero and increasing, and a minimum is when the first derivative is zero and decreasing.

We use a simple ODE, \(y' = sin(x)*e^{-0.05x}\), which has minima and maxima.

from pycse import *
import numpy as np

def ode(y, x):
    return np.sin(x) * np.exp(-0.05 * x)

def minima(y, x):
    '''Approaching a minumum, dydx is negatime and going to zero. our event function is increasing'''
    value = ode(y, x)
    direction = 1
    isterminal = False
    return value,  isterminal, direction

def maxima(y, x):
    '''Approaching a maximum, dydx is positive and going to zero. our event function is decreasing'''
    value = ode(y, x)
    direction = -1
    isterminal = False
    return value,  isterminal, direction

xspan = np.linspace(0, 20, 100)

y0 = 0

X, Y, XE, YE, IE = odelay(ode, y0, xspan, events=[minima, maxima])
print IE
import matplotlib.pyplot as plt
plt.plot(X, Y)

# blue is maximum, red is minimum
colors = 'rb'
for xe, ye, ie in zip(XE, YE, IE):
    plt.plot([xe], [ye], 'o', color=colors[ie])

plt.savefig('./images/ode-events-min-max.png')
plt.show()

[1, 0, 1, 0, 1, 0]

org-mode source

The Kitchin Research Group

Chemical Engineering at Carnegie Mellon University

Finding minima and maxima in ODE solutions with events