The Kitchin Research Group

This ony works for a polynomial, it does not work for any other nonlinear function.

import numpy as np
print np.roots([1, 6, -4, -24])

[-6.  2. -2.]

Let us plot the function to see where the roots are.

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-8, 4)
y = x**3 + 6 * x**2 - 4*x - 24
plt.plot(x, y)
plt.savefig('images/count-roots-1.png')

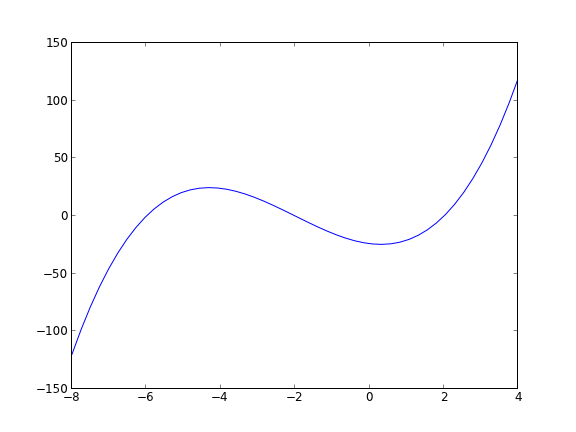
Now we consider several approaches to counting the number of roots in this interval. Visually it is pretty easy, you just look for where the function crosses zero. Computationally, it is tricker.

Count the number of times the sign changes in the interval. What we have to do is multiply neighboring elements together, and look for negative values. That indicates a sign change. For example the product of two positive or negative numbers is a positive number. You only get a negative number from the product of a positive and negative number, which means the sign changed.

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-8, 4)
y = x**3 + 6 * x**2 - 4*x - 24

print np.sum(y[0:-2] * y[1:-1] < 0)

3

This method gives us the number of roots, but not where the roots are.

Using events in an ODE solver python can identify events in the solution to an ODE, for example, when a function has a certain value, e.g. f(x) = 0. We can take advantage of this to find the roots and number of roots in this case. We take the derivative of our function, and integrate it from an initial starting point, and define an event function that counts zeros.

$$f'(x) = 3x^2 + 12x - 4$$

with f(-8) = -120

import numpy as np
from pycse import odelay

def fprime(f, x):
    return 3.0 * x**2 + 12.0*x - 4.0

def event(f, x):
    value = f # we want f = 0
    isterminal = False
    direction = 0
    return value, isterminal, direction

xspan = np.linspace(-8, 4)
f0 = -120

X, F, TE, YE, IE = odelay(fprime, f0, xspan, events=[event])
for te, ye in zip(TE, YE):
    print 'root found at x = {0: 1.3f}, f={1: 1.3f}'.format(te, ye)

root found at x = -6.000, f=-0.000
root found at x = -2.000, f=-0.000
root found at x =  2.000, f= 0.000