The Kitchin Research Group

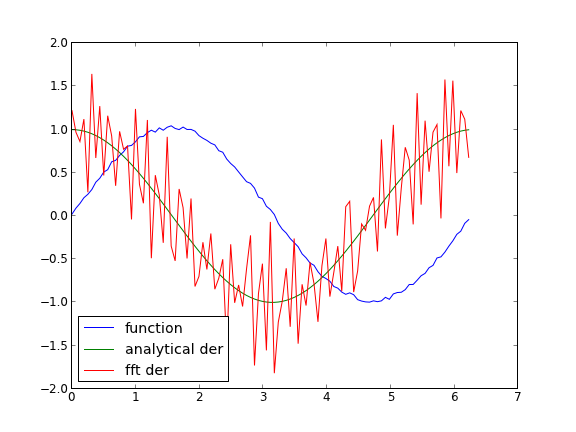
import numpy as np
import matplotlib.pyplot as plt

N = 101 #number of points
L = 2 * np.pi #interval of data

x = np.arange(0.0, L, L/float(N)) #this does not include the endpoint

#add some random noise
y = np.sin(x) + 0.05 * np.random.random(size=x.shape)
dy_analytical = np.cos(x)

'''
http://sci.tech-archive.net/Archive/sci.math/2008-05/msg00401.html

you can use fft to calculate derivatives!
'''

if N % 2 == 0:
    k = np.asarray(range(0, N / 2) + [0] + range(-N / 2 + 1,0))
else:
    k = np.asarray(range(0,(N - 1) / 2) + [0] + range(-(N - 1) / 2, 0))

k *= 2 * np.pi / L

fd = np.real(np.fft.ifft(1.0j * k * np.fft.fft(y)))

plt.plot(x, y, label='function')
plt.plot(x,dy_analytical,label='analytical der')
plt.plot(x,fd,label='fft der')
plt.legend(loc='lower left')

plt.savefig('images/fft-der.png')
plt.show()