Plug flow reactor with a pressure drop

Posted February 18, 2013 at 09:00 AM | categories: ode | tags: reaction engineering, fluids

Updated March 06, 2013 at 04:39 PM

If there is a pressure drop in a plug flow reactor, 1 there are two equations needed to determine the exit conversion: one for the conversion, and one from the pressure drop.

\begin{eqnarray} \frac{dX}{dW} &=& \frac{k'}{F_A0} \left ( \frac{1-X}{1 + \epsilon X} \right) y\\ \frac{dX}{dy} &=& -\frac{\alpha (1 + \epsilon X)}{2y} \end{eqnarray}

Here is how to integrate these equations numerically in python. 

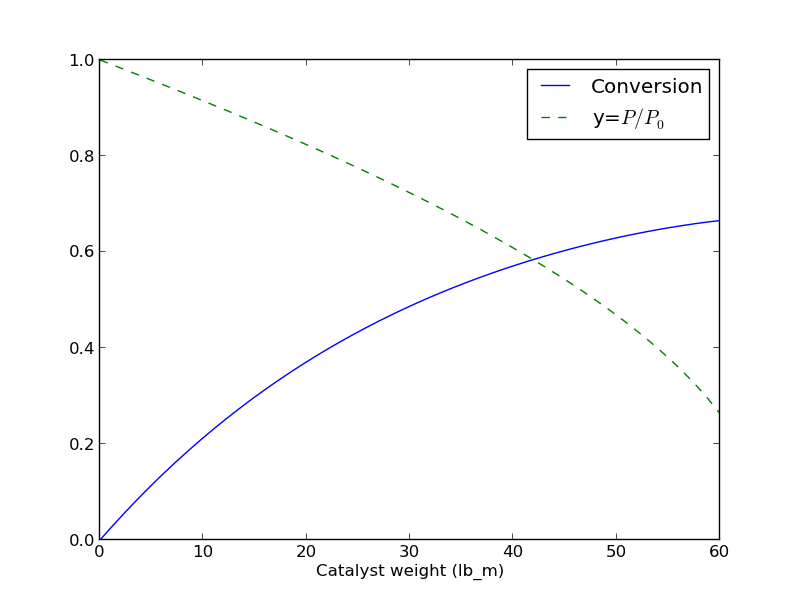
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

kprime = 0.0266
Fa0 = 1.08
alpha = 0.0166
epsilon = -0.15

def dFdW(F, W):
    'set of ODEs to integrate'
    X = F[0]
    y = F[1]
    dXdW = kprime / Fa0 * (1-X) / (1 + epsilon*X) * y
    dydW = -alpha * (1 + epsilon * X) / (2 * y)
    return [dXdW, dydW]

Wspan = np.linspace(0,60)
X0 = 0.0
y0 = 1.0
F0 = [X0, y0]
sol = odeint(dFdW, F0, Wspan)

# now plot the results
plt.plot(Wspan, sol[:,0], label='Conversion')
plt.plot(Wspan, sol[:,1], 'g--', label='y=$P/P_0$')
plt.legend(loc='best')
plt.xlabel('Catalyst weight (lb_m)')
plt.savefig('images/2013-01-08-pdrop.png')

Here is the resulting figure.

Copyright (C) 2013 by John Kitchin. See the License for information about copying.

org-mode source

Discuss on Twitter