The Kitchin Research Group

A photovoltaic device is characterized by a current-voltage relationship. Let us say, for argument's sake, that the relationship is known and defined by

\(i = 0.5 - 0.5 * V^2\)

The voltage is highest when the current is equal to zero, but of course then you get no power. The current is highest when the voltage is zero, i.e. short-circuited, but there is again no power. We seek the highest power condition, which is to find the maximum of \(i V\). This is a constrained optimization. We solve it by creating an objective function that returns the negative of (\i V\), and then find the minimum.

First, let us examine the i-V relationship.

import matplotlib.pyplot as plt
import numpy as np

V = np.linspace(0, 1)

def i(V):
    return 0.5 - 0.5 * V**2

plt.figure()
plt.plot(V, i(V))
plt.savefig('images/iV.png')

<matplotlib.figure.Figure object at 0x11193ec18>
[<matplotlib.lines.Line2D object at 0x111d43668>]

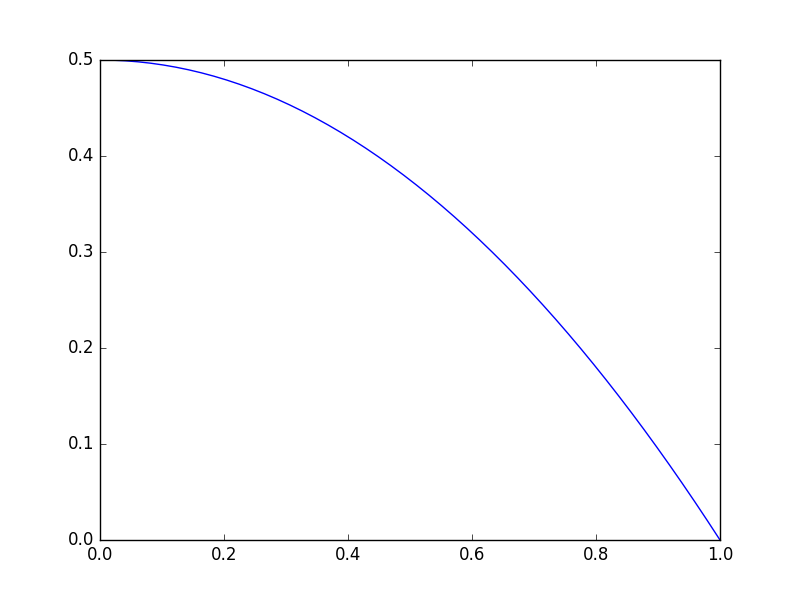
Now, let us be sure there is a maximum in power.

import matplotlib.pyplot as plt
import numpy as np

V = np.linspace(0, 1)

def i(V):
    return 0.5 - 0.5 * V**2

plt.plot(V, i(V) * V)
plt.savefig('images/P1.png')

[<matplotlib.lines.Line2D object at 0x111d437f0>]

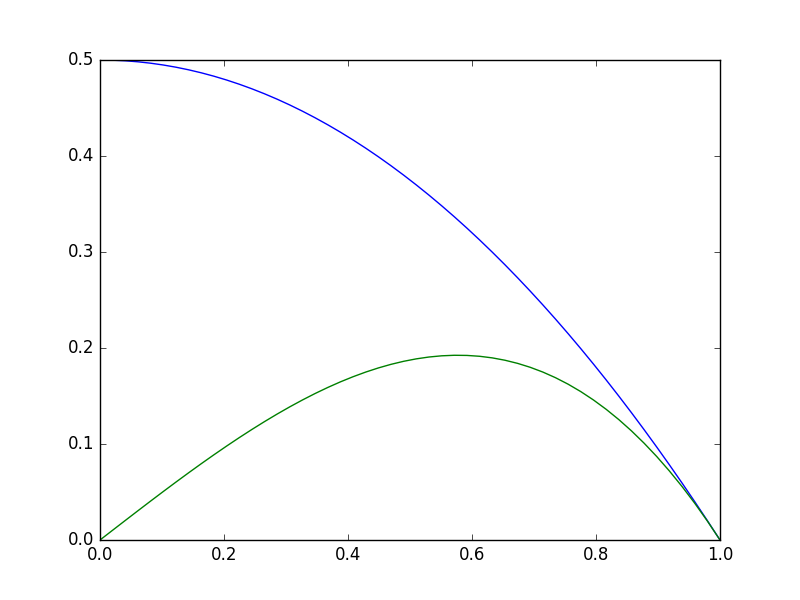
You can see in fact there is a maximum, near V=0.6. We could solve this problem analytically by taking the appropriate derivative and solving it for zero. That still might require solving a nonlinear problem though. We will directly setup and solve the constrained optimization.

from scipy.optimize import fmin_slsqp
import numpy as np
import matplotlib.pyplot as plt

def objective(X):
    i, V = X
    return - i * V

def eqc(X):
    'equality constraint'
    i, V = X
    return (0.5 - 0.5 * V**2) - i

X0 = [0.2, 0.6]
X = fmin_slsqp(objective, X0, eqcons=[eqc])

imax, Vmax = X


V = np.linspace(0, 1)

def i(V):
    return 0.5 - 0.5 * V**2

plt.plot(V, i(V), Vmax, imax, 'ro')
plt.savefig('images/P2.png')

Optimization terminated successfully.    (Exit mode 0)
            Current function value: -0.192450127337
            Iterations: 5
            Function evaluations: 20
            Gradient evaluations: 5
[<matplotlib.lines.Line2D object at 0x111946470>, <matplotlib.lines.Line2D object at 0x11192c518>]

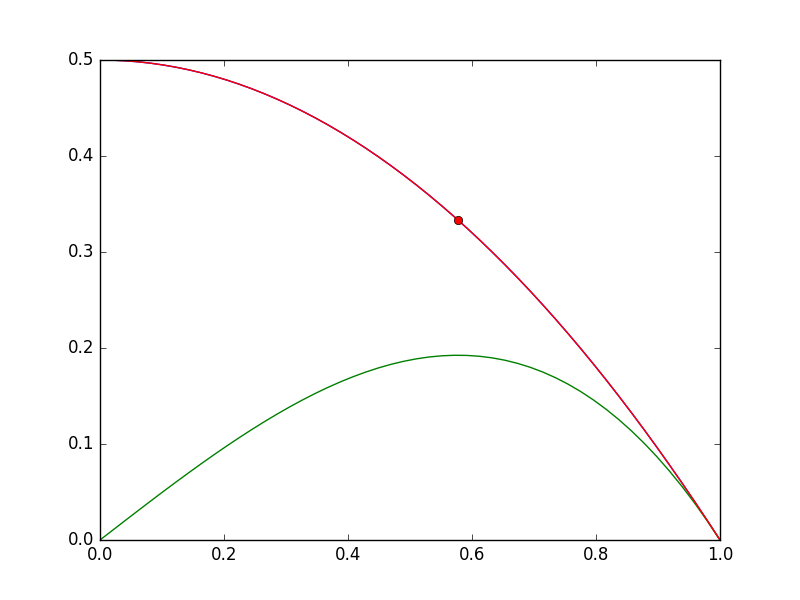
You can see the maximum power is approximately 0.2 (unspecified units), at the conditions indicated by the red dot in the figure above.

Copyright (C) 2016 by John Kitchin. See the License for information about copying.

org-mode source

Org-mode version = 8.2.10