Smooth transitions between two constants
Posted February 27, 2013 at 02:53 PM | categories: math | tags:
Updated March 06, 2013 at 06:26 PM
Suppose we have a parameter that has two different values depending on the value of a dimensionless number. For example when the dimensionless number is much less than 1, x = 2/3, and when x is much greater than 1, x = 1. We desire a smooth transition from 2/3 to 1 as a function of x to avoid discontinuities in functions of x. We will adapt the smooth transitions between functions to be a smooth transition between constants.
We define our function as \(x(D) = x0 + (x1 - x0)*(1 - sigma(D,w)\). We control the rate of the transition by the variable \(w\)
import numpy as np import matplotlib.pyplot as plt x0 = 2.0 / 3.0 x1 = 1.5 w = 0.05 D = np.linspace(0,2, 500) sigmaD = 1.0 / (1.0 + np.exp(-(1 - D) / w)) x = x0 + (x1 - x0)*(1 - sigmaD) plt.plot(D, x) plt.xlabel('D'); plt.ylabel('x') plt.savefig('images/smooth-transitions-constants.png')
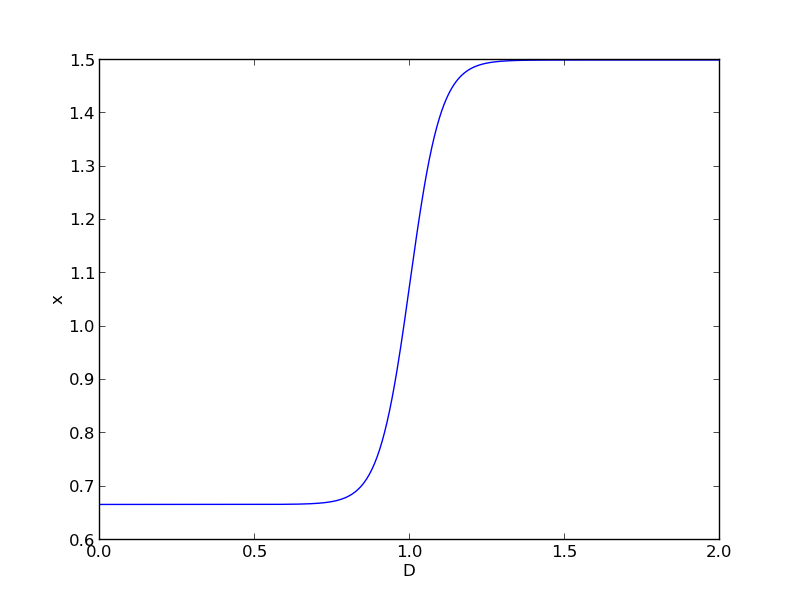
This is a nice trick to get an analytical function with continuous derivatives for a transition between two constants. You could have the transition occur at a value other than D = 1, as well by changing the argument to the exponential function.
Copyright (C) 2013 by John Kitchin. See the License for information about copying.